
分析 根據題意,設M(x0,y0),分析可得P的坐標,分析可得$x_0^2+{(2{y_0})^2}=1$,整理得$\frac{x_0^2}{4}+y_0^2=1$,即可得M的軌跡是橢圓,由橢圓的標準方程分析可得其焦點坐標以及離心率.
解答 解:根據題意,設M(x0,y0),又由線段PD的中點M,則P(x0,2y0),
點P在圓上運動,所以$x_0^2+{(2{y_0})^2}=1$,整理得$\frac{x_0^2}{4}+y_0^2=1$,
所以點M的軌跡是橢圓,
該橢圓的焦點是$({±\sqrt{3},0})$,離心率為$\frac{{\sqrt{3}}}{2}$.
點評 本題考查曲線的軌跡方程,涉及橢圓的幾何性質,關鍵是求出軌跡的方程.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖所示,某中學興趣小組設計的自動小車按下面程序運行:
如圖所示,某中學興趣小組設計的自動小車按下面程序運行:查看答案和解析>>
科目:高中數學 來源: 題型:解答題

查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\{k\left|{k>\frac{{\sqrt{6}}}{3}}\right.或k<-\frac{{\sqrt{6}}}{3}\}$ | B. | $\{k\left|{-\frac{{\sqrt{6}}}{3}<k<\frac{{\sqrt{6}}}{3}}\right.\}$ | C. | $\{k\left|{k≥\frac{{\sqrt{6}}}{3}}\right.或k≤-\frac{{\sqrt{6}}}{3}\}$ | D. | $\{k\left|{-\frac{{\sqrt{6}}}{3}≤k≤\frac{{\sqrt{6}}}{3}}\right.\}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,三棱錐O-ABC中,AO⊥平面OBC,且OA=OB=OC=2,∠BOC=60°,點E,F分別是AB,AC的中點,H為EF的中點,過EF的動平面與線段OA交于點A1,與線段OB,OC的延長線分別相交于點B1,C1.
如圖,三棱錐O-ABC中,AO⊥平面OBC,且OA=OB=OC=2,∠BOC=60°,點E,F分別是AB,AC的中點,H為EF的中點,過EF的動平面與線段OA交于點A1,與線段OB,OC的延長線分別相交于點B1,C1.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
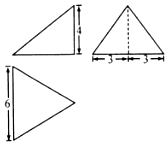 如圖,某三棱錐的正視圖、側視圖和俯視圖分別是直角三角形、等腰三角形和等邊三角形,若該三棱錐的頂點都在同一球面上,則該球的表面積為( )
如圖,某三棱錐的正視圖、側視圖和俯視圖分別是直角三角形、等腰三角形和等邊三角形,若該三棱錐的頂點都在同一球面上,則該球的表面積為( )| A. | 27π | B. | 48π | C. | 64π | D. | 81π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<b<c | B. | a>b>c | C. | b<a<c | D. | b>a>c |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com