
 如圖,三棱錐O-ABC中,AO⊥平面OBC,且OA=OB=OC=2,∠BOC=60°,點E,F分別是AB,AC的中點,H為EF的中點,過EF的動平面與線段OA交于點A1,與線段OB,OC的延長線分別相交于點B1,C1.
如圖,三棱錐O-ABC中,AO⊥平面OBC,且OA=OB=OC=2,∠BOC=60°,點E,F分別是AB,AC的中點,H為EF的中點,過EF的動平面與線段OA交于點A1,與線段OB,OC的延長線分別相交于點B1,C1.分析 (Ⅰ)連結OE、OF,推導出EF⊥OH,EF⊥AH,從而EF⊥面OAH,推導出EF∥面OB1C1,從而EF∥B1C1,由此能證明B1C1⊥平面OAH.
(Ⅱ)取B1C1的中點M,以OM,OA為y,z軸建立空間直角坐標系,利用向量法能求出二面角A-A1E-F的正弦值.
解答 證明:(Ⅰ)連結OE、OF,OE=OF,由題意知AE=AF,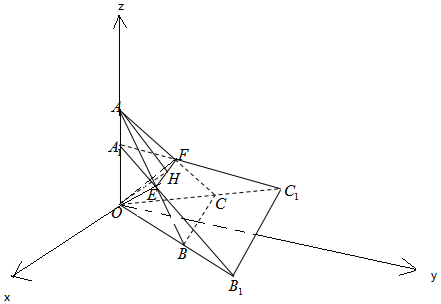
而H為EF中點,∴EF⊥OH,EF⊥AH,
∵OH∩AH=H,∴EF⊥面OAH,
∵EF∥BC,EF?面OB1C${{\;}_{1}}^{\;}$,∴EF∥面OB1C1,
又EF?面A1B1C1,面A1B1C1∩面OB1C1=B1C1,∴EF∥B1C1,
∴B1C1⊥平面OAH.(5分)
解:(Ⅱ)如圖,取B1C1的中點M,以OM,OA為y,z軸建立空間直角坐標系,
由題得$A(0,0,2),B(1,\sqrt{3},0),C(-1,\sqrt{3},0),E(\frac{1}{2},\frac{{\sqrt{3}}}{2},1),F(-\frac{1}{2},\frac{{\sqrt{3}}}{2},1)$,
設|OA1|=h,h∈(1,2),則A1(0,0,h),|BB1|=2h-2,
∴B1(h,$\sqrt{3}h$,0),∵A1,E,B1三點共線,∴A1E∥A1B1,
∴$\overrightarrow{{A}_{1}E}$與$\overrightarrow{{A}_{1}{B}_{1}}$平行,∴$\frac{h}{\frac{1}{2}}=\frac{\sqrt{3}h}{\frac{\sqrt{3}}{2}}=\frac{-h}{1-h}$,解得h=$\frac{3}{2}$,∴${A_1}(0,0,\frac{3}{2})$,
$\overrightarrow{A{A}_{1}}$=(0,0,-$\frac{1}{2}$),$\overrightarrow{AE}$=($\frac{1}{2},\frac{\sqrt{3}}{2}$,-1),
設平面面AA1E的法向量為$\overrightarrow{n}$=(x,y,z),
則$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{A{A}_{1}}=-\frac{1}{2}z=0}\\{\overrightarrow{n}•\overrightarrow{AE}=\frac{1}{2}x+\frac{\sqrt{3}}{2}y-z=0}\end{array}\right.$,取x=$\sqrt{3}$,得$\overrightarrow{n}$=($\sqrt{3},-1,0$),
同理得面A1EF的法向量為$\overrightarrow{m}$=(0,1,$\sqrt{3}$),
設二面角A-A1E-F的平面角為θ,
則|cosθ|=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{1}{4}$,則sinθ=$\frac{\sqrt{15}}{4}$,
∴二面角A-A1E-F的正弦值為$\frac{\sqrt{15}}{4}$.(12分)
點評 本題考查線面垂直的證明,考查二面角的正弦值的求法,考查空間中線線、線面、面面間的位置關系等基礎知識,考查推理論證能力、運算求解能力、空間想象能力,考查化歸與轉化思想、函數與方程思想、數形結合思想,是中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
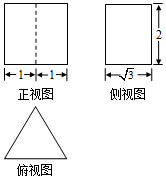
| A. | 12 | B. | 8+2$\sqrt{3}$ | C. | 12+2$\sqrt{3}$ | D. | 12+4$\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com