
分析 對任意的n∈N*,滿足${a_{n+2}}-{a_n}≤{3^n},{a_{n+4}}-{a_n}≥10×{3^n}$,可得10×3n≤(an+4-an+2)+(an+2-an)≤3n+2+3n=10×3n.an+4-an=10×3n.利用a2017=(a2017-a2013)+(a2013-a2009)+…+(a5-a1)+a1與等比數列的求和公式即可得出.
解答 解:∵對任意的n∈N*,滿足${a_{n+2}}-{a_n}≤{3^n},{a_{n+4}}-{a_n}≥10×{3^n}$,
∴10×3n≤(an+4-an+2)+(an+2-an)≤3n+2+3n=10×3n.
∴an+4-an=10×3n.
∴a2017=(a2017-a2013)+(a2013-a2009)+…+(a5-a1)+a1
=10×(32013+32009+…+3)+$\frac{3}{8}$
=10×$\frac{3×(8{1}^{504}-1)}{81-1}$+$\frac{3}{8}$=$\frac{{3}^{2017}}{8}$.
故答案為:$\frac{{{3^{2017}}}}{8}$.
點評 本題考查了數列遞推關系、等比數列的通項公式與求和公式、累加求和方法,考查了推理能力與計算能力,屬于難題.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $-\frac{4}{3}$ | D. | -3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
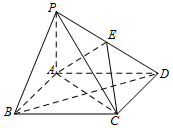 如圖,在四棱錐P-ABCD中,PA=AB=$\frac{1}{2}$AD=2,PB=2$\sqrt{2}$,PA⊥AD,底面ABCD為平行四邊形,∠ADC=60°,E為PD的中點.
如圖,在四棱錐P-ABCD中,PA=AB=$\frac{1}{2}$AD=2,PB=2$\sqrt{2}$,PA⊥AD,底面ABCD為平行四邊形,∠ADC=60°,E為PD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{y^2}{4}-\frac{x^2}{12}=1$ | C. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | D. | $\frac{y^2}{12}-\frac{x^2}{4}=1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com