
分析 (1)由已知利用行列式的計算,三角函數恒等變換的應用化簡可得函數解析式f(x)=sin(2x+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$,結合范圍2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{4π}{3}$],利用正弦函數的性質即可得解值域.
(2)由已知可求sin(A+$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$,結合范圍A+$\frac{π}{3}$∈($\frac{π}{3}$,$\frac{4π}{3}$),可得A=$\frac{π}{3}$,由余弦定理解得:bc=3,利用三角形面積公式即可計算得解.
解答 (本題滿分為14分,第1小題滿分為6分,第2小題滿分為8分)
解:(1)∵f(x)=$|\begin{array}{l}{\sqrt{3}co{s}^{2}x}&{-sinx}\\{cosx}&{1}\end{array}|$=$\sqrt{3}$cos2x+sinxcosx=sin(2x+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$,
∵x∈[0,$\frac{π}{2}$],2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{4π}{3}$],
∴sin(2x+$\frac{π}{3}$)∈[-$\frac{\sqrt{3}}{2}$,1],可得:f(x)=sin(2x+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$∈[0,1+$\frac{\sqrt{3}}{2}$].
(2)∵f($\frac{A}{2}$)=sin(A+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,可得:sin(A+$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$,
∵A∈(0,π),A+$\frac{π}{3}$∈($\frac{π}{3}$,$\frac{4π}{3}$),可得:A+$\frac{π}{3}$=$\frac{2π}{3}$,解得:A=$\frac{π}{3}$.
∵a=4,b+c=5,
∴由余弦定理a2=b2+c2-2bccosA,可得:16=b2+c2-bc=(b+c)2-3bc=25-3bc,解得:bc=3,
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}×$3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$.
點評 本題主要考查了行列式的計算,三角函數恒等變換的應用,正弦函數的圖象和性質,余弦定理,三角形面積公式在解三角形中的綜合應用,考查了計算能力和轉化思想,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分非必要條件 | B. | 必要非充分條件 | ||
| C. | 充要條件 | D. | 既非充分也非必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
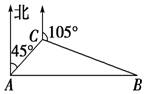 一商船行至索馬里海域時,遭到海盜的追擊,隨即發出求救信號.正在該海域執行護航任務的海軍“黃山”艦在A處獲悉后,即測出該商船在方位角為45°距離10海里的C處,并沿方位角為105°的方向,以9海里/時的速度航行.“黃山”艦立即以21海里/時的速度前去營救.如圖所示,求“黃山”艦靠近商船所需要的最少時間及所經過的路程.
一商船行至索馬里海域時,遭到海盜的追擊,隨即發出求救信號.正在該海域執行護航任務的海軍“黃山”艦在A處獲悉后,即測出該商船在方位角為45°距離10海里的C處,并沿方位角為105°的方向,以9海里/時的速度航行.“黃山”艦立即以21海里/時的速度前去營救.如圖所示,求“黃山”艦靠近商船所需要的最少時間及所經過的路程.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com