
分析 ①由${a_1}=\frac{1}{2},{a_n}+2{S_n}{S_{n-1}}=0(n≥2)$.可得Sn-Sn-1+2SnSn-1=0,化為:$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,即可證明.
②利用等差數列的通項公式即可得出.
③n≥2時,${S}_{n}^{2}$=$\frac{1}{4{n}^{2}}$<$\frac{1}{4}\frac{1}{n(n-1)}$=$\frac{1}{4}(\frac{1}{n-1}-\frac{1}{n})$.利用“裂項求和”與數列的單調性即可得出.
解答 ①解:∵${a_1}=\frac{1}{2},{a_n}+2{S_n}{S_{n-1}}=0(n≥2)$.
∴Sn-Sn-1+2SnSn-1=0,化為:$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,
∴數列$\left\{{\frac{1}{S_n}}\right\}$為等差數列,公差為2,首項為2.
②解:$\frac{1}{{S}_{n}}$=2+2(n-1)=2n.
∴Sn=$\frac{1}{2n}$.
③證明:n≥2時,${S}_{n}^{2}$=$\frac{1}{4{n}^{2}}$<$\frac{1}{4}\frac{1}{n(n-1)}$=$\frac{1}{4}(\frac{1}{n-1}-\frac{1}{n})$.
∴${S}_{1}^{2}+{S}_{2}^{2}$+…+${S}_{n}^{2}$≤$\frac{1}{4}$+$\frac{1}{4}$$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n-1}-\frac{1}{n})]$=$\frac{1}{2}-\frac{1}{n}$<$\frac{1}{2}$.
點評 本題考查了等差數列的定義通項公式、“裂項求和”與數列的單調性、數列遞推關系,考查了推理能力與計算能力,屬于中檔題.


 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | M>N | B. | M<N | C. | M≥N | D. | M≤N |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
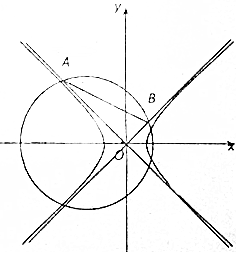 如圖,雙曲線k2x2-y2=1(k>0)的兩條漸近線與圓(x+2)2+y2=5在x軸的上方交于A、B兩點.
如圖,雙曲線k2x2-y2=1(k>0)的兩條漸近線與圓(x+2)2+y2=5在x軸的上方交于A、B兩點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com