
分析 (1)運用兩角差的余弦公式和二倍角公式,化簡可得f(x),再由余弦函數的單調區間,解不等式可得所求增區間;
(2)求得f(x)的最值,即可得到a的取值范圍.
解答 解:(1)函數$f(x)=cosx•cos(x-\frac{π}{3})$=cosx($\frac{1}{2}$cosx+$\frac{\sqrt{3}}{2}$sinx)
=$\frac{1+cos2x}{4}$+$\frac{\sqrt{3}}{4}$sin2x=$\frac{1}{2}$cos(2x-$\frac{π}{3}$)+$\frac{1}{4}$,
由2kπ-π≤2x-$\frac{π}{3}$≤2kπ,k∈Z,
解得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,k∈Z,
即f(x)的增區間為[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z;
(2)由(1)可得當2x-$\frac{π}{3}$=2kπ,即x=kπ+$\frac{π}{6}$,k∈Z時,f(x)取得最大值$\frac{3}{4}$;
當2x-$\frac{π}{3}$=2kπ+π,即x=kπ+$\frac{2π}{3}$,k∈Z時,f(x)取得最小值-$\frac{1}{4}$.
由直線y=a與函數f(x)的圖象無公共點,
可得a的范圍是a>$\frac{3}{4}$或a<-$\frac{1}{4}$.
點評 本題考查三角函數的化簡和求值,考查余弦函數的圖象和性質,屬于中檔題.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數學 來源: 題型:選擇題
| A. | p2,p3 | B. | p1,p4 | C. | p1,p2 | D. | p1,p3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
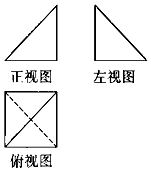 如圖1,一個多面體的正視圖和側視圖是兩個全等的等腰直角三角形且直角邊長為2,俯視圖是邊長為2的正方形,則該多面體的表面積是( )
如圖1,一個多面體的正視圖和側視圖是兩個全等的等腰直角三角形且直角邊長為2,俯視圖是邊長為2的正方形,則該多面體的表面積是( )| A. | $2+4\sqrt{2}+2\sqrt{3}$ | B. | $2+4\sqrt{2}+\sqrt{6}$ | C. | $2+4\sqrt{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 奇函數,且在區間$(0,\frac{π}{2})$上單調遞增 | B. | 奇函數,且在區間$(0,\frac{π}{2})$上單調遞減 | ||
| C. | 偶函數,且在區間$(0,\frac{π}{2})$上單調遞增 | D. | 偶函數,且在區間$(0,\frac{π}{2})$上單調遞減 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)+g(x)是偶函數 | B. | f(x)•g(x)是偶函數 | C. | f(x)+g(x)是奇函數 | D. | f(x)•g(x)是奇函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com