Question

10．在長方體ABCD-A₁B₁C₁D₁中，AB=BC=$\sqrt{2}$AA₁，Q是棱CC₁上的動點，則當BQ+QD₁的長度取得最小值時，直線B₁Q與直線AD所成角的正切值為$\frac{\sqrt{2}}{4}$．

Answer 1

分析 當BQ+D₁Q的長度取得最小值時Q是CC₁的中點，以D₁為原點，D₁A₁為x軸，D₁C₁為y軸，D₁D為z軸，建立空間直角坐標系，利用向量法能求出直線B₁Q和直AD所成的角的正切值．

解答 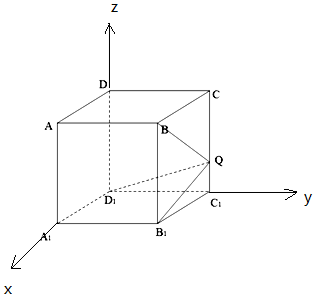解：設AB=BC=$\sqrt{2}$AA₁=$\sqrt{2}$，
把B₁C₁CB展開與D₁C₁CD成一個長方形D₁B₁BD時，
連結D₁B，交CC₁于Q時，當BQ+D₁Q的長度取得最小值，
此時Q是CC₁的中點，
以D₁為原點，D₁A₁為x軸，D₁C₁為y軸，D₁D為z軸，建立空間直角坐標系，
${B}_{1}（\sqrt{2}，\sqrt{2}，0）$，Q（0，$\sqrt{2}$，$\frac{1}{2}$），A（ $\sqrt{2}，0，1）$，D（0，0，1），
$\overrightarrow{AD}=（-\sqrt{2}，0，0）$，$\overrightarrow{{B}_{1}Q}=（-\sqrt{2}，0，\frac{1}{2}）$
cos$＜\overrightarrow{AD}，\overrightarrow{{B}_{1}Q}＞$=$\frac{\overrightarrow{AD}•\overrightarrow{{B}_{1}Q}}{|\overrightarrow{AD}||\overrightarrow{{B}_{1}Q}|}$=$\frac{2}{\sqrt{2}×\frac{3}{2}}=\frac{2\sqrt{2}}{3}$．
設直線B₁Q和直線AD所成角為θ，則cos$θ=\frac{2\sqrt{2}}{3}$，tanθ=$\frac{\sqrt{2}}{4}$
故答案為：$\frac{\sqrt{2}}{4}$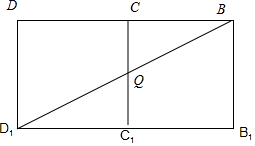

點評 本題考查線線角的正切值的求法，是中檔題，解題時要認真審題，注意空間思維能力的培養．