
| A. | (2,+∞) | B. | ($\frac{5}{2}$,+∞) | C. | (2,$\frac{5}{2}$) | D. | [2,$\frac{5}{2}$) |
分析 由題,y=g(f(x))的圖象與y=a的圖象有四個不同的交點,由于復合函數圖象不容易作圖,則用換元法將復合函數分解為兩個函數.令t=f(x),則y=g(t),由y=g(t)與y=a的交點個數,確定t的值及個數,再根據t的值確定t=f(x)的根x的個數,即為函數y=g(f(x))的零點的個數.
解答 
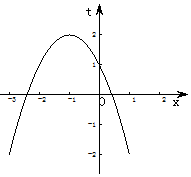 解:令t=f(x)=-(x+1)2+2,t≤2,
解:令t=f(x)=-(x+1)2+2,t≤2,
則y=g(f(x))=g(t)=$\left\{\begin{array}{l}{t+\frac{1}{t},0<t≤2}\\{3-(\frac{1}{2})t,t≤0}\end{array}\right.$,
由題,y=g(f(x))-a的圖象恰有四個不同的零點,
等價于關于x的方程g(f(x))=a有4個不同的根,
等價于關于t的方程g(t)=a的根使得關于x的方程t=f(x)共有四個不同的根.
∵t=2時,y=2.5;且函數y=g(t)、t=f(x)的圖象如圖所示.
∴對a分類如下:
①a=2時,t1=1或t2=0,
此時函數y=g(f(x))-a有四個零點,符合;
②2<a<2.5時,方程a=g(t)有兩個不同的根,且t1∈(0,1)或t2∈(1,2),
此時函數y=g(f(x))-a有四個零點,符合;
③a=2.5時,t1=2或t2=0.5
當t=2時,方程t=f(x)有且只有一個根,當t=0.5時,方程t=f(x)有兩個根,
故此時函數y=g(f(x))-a有三個零點,不符合;
④a>2.5時,方程a=g(t)有且只有一個根,且t∈(0,1),
此時函數y=g(f(x))-a有兩個零點,不符合;
⑤a<2時,方程a=g(t)有且只有一個根,且t∈(-∞,0),
此時函數y=g(f(x))-a有兩個零點,不符合;
綜上所述,當2≤a<2.5時,函數y=g(f(x))-a有四個零點.
故選:D.
點評 考查函數零點的化歸思想和數形結合思想,復合函數用換元法轉化為兩個基礎函數,避免作復合函數的圖象,研究零點個數的方法.屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y2=-2x | B. | y2=-4x | C. | y2=2x | D. | y2=-4x或y2=-36x |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
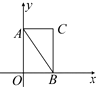 已知Rt△ABC的三邊長分別為AB=5,BC=4,AC=3,在平面直角坐標系中,△ABC的初始位置如圖(圖中CB⊥x軸),現將△ABC沿x軸滾動,設點A(x,y)的軌跡方程是y=f(x),則f(2017)=( )
已知Rt△ABC的三邊長分別為AB=5,BC=4,AC=3,在平面直角坐標系中,△ABC的初始位置如圖(圖中CB⊥x軸),現將△ABC沿x軸滾動,設點A(x,y)的軌跡方程是y=f(x),則f(2017)=( )| A. | $\sqrt{21}$ | B. | $2\sqrt{6}$ | C. | 4 | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 所有著名的作家可以形成一個集合 | |
| B. | 0與 {0}的意義相同 | |
| C. | 集合A={x|x=$\frac{1}{n}$,n∈N*} 是有限集 | |
| D. | 方程x2+2x+1=0的解集只有一個元素 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(\frac{4}{3},2)$ | B. | $[\frac{4}{3},2)$ | C. | $(-∞,\frac{4}{3})∪(2,+∞)$ | D. | $(-∞,\frac{4}{3}]∪(2,+∞)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com