
分析 (1)化簡不等式,利用指數不等式轉化為一次不等式,求解即可.
(2)利用函數恒成立,轉化為不等式組,求解即可.
解答 解:(1)由于$a=\frac{{\sqrt{2}}}{2}={2^{-\frac{1}{2}}}$,于是不等式f(x)<0即為${2^{2x-7}}<{2^{-\frac{1}{2}({4x-1})}}$,…(2分)
所以$2x-7<-\frac{1}{2}({4x-1})$,解得$x<\frac{15}{8}$.…(4分)
即原不等式的解集為$({-∞\;\;,\;\;\frac{15}{8}})$.…(5分)
(2)由${2^{2x-7}}<{a^{4x-1}}⇒({2x-7})lg2<({4x-1})lga⇒x•lg\frac{4}{a^4}+lg\frac{a}{128}<0$.…(7分)
設$f(x)=x•lg\frac{4}{a^4}+lg\frac{a}{128}$,則f(x)為一次函數或常數函數,由x∈[0,1]時,f(x)<0恒成立得:$\left\{\begin{array}{l}f(1)<0\\ f(0)<0\end{array}\right.⇒\left\{\begin{array}{l}lg\frac{4}{a^4}+lg\frac{a}{128}<0\\ lg\frac{a}{128}<0\end{array}\right.⇒\left\{\begin{array}{l}lg\frac{1}{{32{a^3}}}<0\\ 0<a<128\end{array}\right.⇒\left\{\begin{array}{l}32{a^3}>1\\ 0<a<128\end{array}\right.⇒\frac{{\root{3}{2}}}{4}<a<128$,
又a>0且a≠1,
∴$a∈({\frac{{\root{3}{2}}}{4}\;\;,\;\;1})∪({1\;\;,\;\;128})$.…(12分)
點評 本題考查函數恒成立,指數不等式的解法,考查轉化思想以及計算能力.


科目:高中數學 來源: 題型:解答題
| 甲 | 8 | 6 | 7 | 8 | 6 | 5 | 9 | 10 | 4 | 7 |
| 乙 | 6 | 7 | 7 | 8 | 6 | 7 | 8 | 7 | 9 | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [0,$\frac{1}{5})$ | B. | ($\frac{1}{5},\frac{1}{4}$) | C. | ($\frac{1}{5},\frac{1}{3}$) | D. | [l,3] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
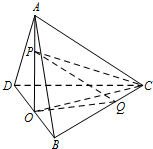 如圖,在三棱錐A-BCD中,BC=DC=AB=AD=2,BD=2$\sqrt{2}$,平面ABD⊥平面BCD,O為BD中點,點P,Q分別為線段AO,BC上的動點(不含端點),且AP=CQ,則三棱錐P-QCO體積的最大值為( )
如圖,在三棱錐A-BCD中,BC=DC=AB=AD=2,BD=2$\sqrt{2}$,平面ABD⊥平面BCD,O為BD中點,點P,Q分別為線段AO,BC上的動點(不含端點),且AP=CQ,則三棱錐P-QCO體積的最大值為( )| A. | $\frac{1}{12}$ | B. | $\frac{\sqrt{2}}{48}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p∧q | B. | (¬p)∧(¬q) | C. | p∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [$\frac{π}{6}$,$\frac{5π}{6}$] | B. | [$\frac{π}{6}$,6] | C. | [$\frac{5π}{6}$,6] | D. | [0,$\frac{π}{6}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{3}$ | B. | $\frac{11}{17}$ | C. | $\frac{12}{19}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (2,+∞) | B. | ($\frac{5}{2}$,+∞) | C. | (2,$\frac{5}{2}$) | D. | [2,$\frac{5}{2}$) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com