
分析 (1)利用函數(shù)f(x)在x=-1處取得極值,求出a;
(2)若g(x)=f(x)-m有3個(gè)零點(diǎn),只需直線y=m與y=f(x)的圖象有三個(gè)不同的交點(diǎn),則說(shuō)明m小于極大值,大于極小值.
解答 解:(1)函數(shù)的導(dǎo)數(shù)為f'(x)=3x2-3a,因?yàn)閒(x)在x=-1處取得極值,
所以f'(-1)=0,即3-3a=0,解得a=1.
(2)由(1)得:f(x)=x3-3x-1,
f'(x)=3x2-3=3(x2-1)=3(x-1)(x+1),
當(dāng)f'(x)>0,得x>1或x<-1.當(dāng)f'(x)<0,得-1<x<1.
即函數(shù)在x=-1處取得極大值f(-1)=1,在x=1處取得極小值f(1)=-3,
如圖示: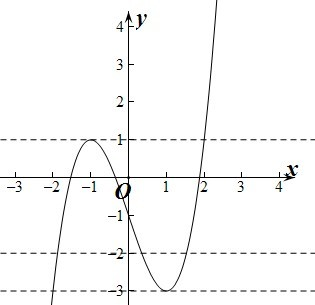 ,
,
若g(x)=f(x)-m有3個(gè)零點(diǎn),
只需直線y=m與y=f(x)的圖象有三個(gè)不同的交點(diǎn),
則m小于極大值,大于極小值,
即-3<m<1,所以m的取值范圍是(-3,1).
點(diǎn)評(píng) 本題的考點(diǎn)是利用導(dǎo)數(shù)研究函數(shù)的極值,以及函數(shù)的交點(diǎn)問(wèn)題.要注意利用數(shù)形結(jié)合的數(shù)學(xué)思想去解決.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{16}$ | D. | 0 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. |  | B. | 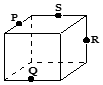 | C. | 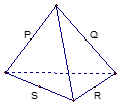 | D. |  |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 4${∫}_{0}^{a}$xf(x)dx | B. | 2${∫}_{0}^{a}$x[f(x)+f(-x)]dx | C. | 0 | D. | 以上都不正確 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | k的最大值為2 | B. | k的最小值為2 | C. | k的最大值為1 | D. | k的最小值為1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 1 | B. | $\frac{8}{9}$ | C. | $\frac{20}{9}$ | D. | 4 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com