
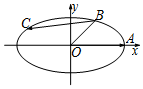
 如圖,橢圓的方程為$\frac{x^2}{6}+\frac{y^2}{2}$=1,A是其右頂點,B是該橢圓在第一象限部分上的一點,且∠AOB=$\frac{π}{4}$.若點C是橢圓上的動點,則$\overrightarrow{OA}•\overrightarrow{BC}$的取值范圍為[-9,3].
如圖,橢圓的方程為$\frac{x^2}{6}+\frac{y^2}{2}$=1,A是其右頂點,B是該橢圓在第一象限部分上的一點,且∠AOB=$\frac{π}{4}$.若點C是橢圓上的動點,則$\overrightarrow{OA}•\overrightarrow{BC}$的取值范圍為[-9,3]. 分析 由由橢圓的方程為$\frac{x^2}{6}+\frac{y^2}{2}$=1焦點在x軸上,A點坐標為($\sqrt{6}$,0),直線OB所在的直線為:y=x,設B點坐標為(x,x),代入即可求得B點坐標,設C點坐標為($\sqrt{6}$cosθ,$\sqrt{2}$sinθ),則$\overrightarrow{OA}•\overrightarrow{BC}$=($\sqrt{6}$,0)•($\sqrt{6}$cosθ-$\frac{\sqrt{6}}{2}$,$\sqrt{2}$sinθ-$\frac{\sqrt{6}}{2}$)=6cosθ-3,由余弦函數的性質,即可求得$\overrightarrow{OA}•\overrightarrow{BC}$的取值范圍.
解答 解:由橢圓的方程為$\frac{x^2}{6}+\frac{y^2}{2}$=1焦點在x軸上,A點坐標為($\sqrt{6}$,0),∵∠AOB=$\frac{π}{4}$,
∴直線OB所在的直線為:y=x,
設B點坐標為(x,x),
將B點坐標代入到橢圓方程里,有:$\frac{{x}^{2}}{6}+\frac{{x}^{2}}{4}=1$
解得:x2=$\frac{3}{2}$,x=$\frac{\sqrt{6}}{2}$
∴B點坐標為($\frac{\sqrt{6}}{2}$,$\frac{\sqrt{6}}{2}$)
設C點坐標為($\sqrt{6}$cosθ,$\sqrt{2}$sinθ)
$\overrightarrow{OA}•\overrightarrow{BC}$=($\sqrt{6}$,0)•($\sqrt{6}$cosθ-$\frac{\sqrt{6}}{2}$,$\sqrt{2}$sinθ-$\frac{\sqrt{6}}{2}$)=6cosθ-3,
∵cosθ∈[-1,1],
∴當cosθ=-1時,$\overrightarrow{OA}•\overrightarrow{BC}$取最小值,最小值為-6-3=-9,
當cosθ=1時,$\overrightarrow{OA}•\overrightarrow{BC}$取最大值,最大值為6-3=3,
$\overrightarrow{OA}•\overrightarrow{BC}$的取值范圍[-9,3].
故答案為:[-9,3].
點評 本題考查橢圓的參數方程,直線與橢圓的關系,考查向量數量積的坐標運算,余弦函數的最值,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=x0與f(x)=1 | B. | f(x)=$\sqrt{{x}^{2}}$-1與f(x)=|x|-1 | ||
| C. | f(x)=$\frac{{x}^{2}-4}{x+2}$與f(x)=x-2 | D. | f(x)=$\sqrt{(x-1)(x-2)}$與f(x)=$\sqrt{x-1}$$\sqrt{x-2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
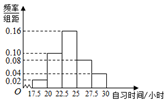 某中學調查200名學生每周晚自習時間(單位,小時),制成了如圖所示頻率分布直方圖,其中自習時間的范圍為[17.5,30],根據直方圖,這200名學生每周自習時間不少于22.5小時的人數是140.
某中學調查200名學生每周晚自習時間(單位,小時),制成了如圖所示頻率分布直方圖,其中自習時間的范圍為[17.5,30],根據直方圖,這200名學生每周自習時間不少于22.5小時的人數是140.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com