
分析 (I)直線l的參數方程$\left\{\begin{array}{l}x=3+\frac{4}{5}t\\ y=3+\frac{3}{5}t\end{array}\right.$(t為參數),消去參數化為普通方程,利用點到直線的距離公式可得:原點(0,0)到直線l的距離d.
(II)圓錐曲線C的參數方程為$\left\{\begin{array}{l}x=cosθ\\ y=sinθ\end{array}\right.$(θ為參數),即x2+y2=1.把直線l的方程代入化為:5t2+42t+85=0,利用|PA|•|PB|=|t1t2|即可得出.
解答 解:(I)直線l的參數方程$\left\{\begin{array}{l}x=3+\frac{4}{5}t\\ y=3+\frac{3}{5}t\end{array}\right.$(t為參數),消去參數化為:3x-4y+3=0,
∴原點(0,0)到直線l的距離d=$\frac{3}{5}$.
(II)圓錐曲線C的參數方程為$\left\{\begin{array}{l}x=cosθ\\ y=sinθ\end{array}\right.$(θ為參數),即x2+y2=1.
把直線l的方程代入化為:5t2+42t+85=0,∴t1t2=17.
∴|PA|•|PB|=|t1t2|=17.
點評 本題考查了參數方程化為普通方程、點到直線的距離公式、一元二次方程的根與系數的關系,考查了推理能力與計算能力,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?x0>0,x02≤x0 | B. | ?x∈R,3x>0 | ||
| C. | ?x0∈R,sinx0+cosx0=2 | D. | ?x0∈R,lgx0=0 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
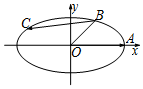 如圖,橢圓的方程為$\frac{x^2}{6}+\frac{y^2}{2}$=1,A是其右頂點,B是該橢圓在第一象限部分上的一點,且∠AOB=$\frac{π}{4}$.若點C是橢圓上的動點,則$\overrightarrow{OA}•\overrightarrow{BC}$的取值范圍為[-9,3].
如圖,橢圓的方程為$\frac{x^2}{6}+\frac{y^2}{2}$=1,A是其右頂點,B是該橢圓在第一象限部分上的一點,且∠AOB=$\frac{π}{4}$.若點C是橢圓上的動點,則$\overrightarrow{OA}•\overrightarrow{BC}$的取值范圍為[-9,3].查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
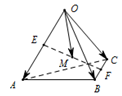 如圖,E,F分別是四面體OABC的邊OA,BC的中點,M為EF的中點,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,則下列向量中與$\overrightarrow{OM}$相等的向量是( )
如圖,E,F分別是四面體OABC的邊OA,BC的中點,M為EF的中點,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,則下列向量中與$\overrightarrow{OM}$相等的向量是( )| A. | -$\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | B. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | D. | -$\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 零件個數x(個) | 1 | 2 | 3 | 4 |
| 加工時間y(小時) | 2 | 3 | 5 | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com