
| A. | [$\frac{5}{4}$,$\frac{5}{3}$] | B. | [$\frac{3}{2}$,++∞) | C. | (1,4] | D. | [$\frac{3}{2}$,4] |
分析 如圖所示,設雙曲線C2的離心率為e1,橢圓與雙曲線的半焦距為c.由橢圓的定義及其題意可得:|MF2|=|F1F2|=2c,|MF1|=2a-2c.由雙曲線的定義可得:2a-2c-2c=2a1,即a-2c=a1,可得$\frac{1}{e}$-2=$\frac{1}{{e}_{1}}$,利用e∈[$\frac{3}{8}$,$\frac{4}{9}$],即可得出雙曲線C2的離心率的取值范圍.
解答 解:如圖所示,
設雙曲線C2的離心率為e1.
橢圓與雙曲線的半焦距為c.
由橢圓的定義及其題意可得:|MF2|=|F1F2|=2c,|MF1|=2a-2c.
由雙曲線的定義可得:2a-2c-2c=2a1,即a-2c=a1,
∴$\frac{1}{e}$-2=$\frac{1}{{e}_{1}}$,
∵e∈[$\frac{3}{8}$,$\frac{4}{9}$],∴$\frac{1}{e}$∈[$\frac{9}{4}$,$\frac{8}{3}$],
∴$\frac{1}{{e}_{1}}$∈[$\frac{1}{4}$,$\frac{2}{3}$].
∴e1∈[$\frac{3}{2}$,4].
故選:D.
點評 本題考查了橢圓與雙曲線的定義標準方程及其性質,考查了推理能力與計算能力,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
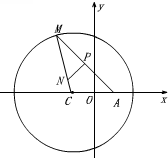 已知圓C:(x+1)2+y2=8,定點A(1,0),M為圓上一動點,線段MA的垂直平分線交MC于點N,設點N的軌跡為曲線E.
已知圓C:(x+1)2+y2=8,定點A(1,0),M為圓上一動點,線段MA的垂直平分線交MC于點N,設點N的軌跡為曲線E.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-1)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-1,0)∪(1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com