
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 由已知向量的坐標求出向量的模,再求出$\overrightarrow{BA}•\overrightarrow{BC}$,代入數量積求夾角公式得答案.
解答 解:∵$\overrightarrow{BA}$=(-$\frac{1}{2},\frac{\sqrt{3}}{2}$),$\overrightarrow{BC}$=($\frac{1}{2},\frac{\sqrt{3}}{2}$),
∴$|\overrightarrow{BA}|=\sqrt{(-\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}=1$,$|\overrightarrow{BC}|=\sqrt{(\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}=1$,
$\overrightarrow{BA}•\overrightarrow{BC}=-\frac{1}{2}×\frac{1}{2}+\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{2}=\frac{1}{2}$,
則cos∠ABC=cos<$\overrightarrow{BA},\overrightarrow{BC}$>=$\frac{\overrightarrow{BA}•\overrightarrow{BC}}{|\overrightarrow{BA}||\overrightarrow{BC}|}=\frac{\frac{1}{2}}{1×1}=\frac{1}{2}$,
則∠ABC=60°.
故選:C.
點評 本題考查平面向量的數量積運算,考查由數量積求向量的夾角,是中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{8\sqrt{3}}}{3}$ | B. | $\frac{{4\sqrt{3}}}{3}$ | C. | $2\sqrt{3}$ | D. | $2\sqrt{15}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,側棱垂直于底面的三棱柱ABC-A1B1C1的各棱長均為2,其正視圖如圖所示,則此三棱柱側視圖的面積為( )
如圖,側棱垂直于底面的三棱柱ABC-A1B1C1的各棱長均為2,其正視圖如圖所示,則此三棱柱側視圖的面積為( )| A. | 2 | B. | 4 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{\sqrt{6}}{3}$ | B. | -$\frac{1}{3}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
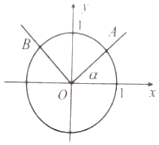 如圖,角α的始邊與x軸的非負半軸重合,終邊與單位圓交于點A(x1,y1),角β=α+$\frac{2π}{3}$的終邊與單位圓交于點B(x2,y2),記f(α)=y1-y2.若角α為銳角,則f(α)的取值范圍是(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
如圖,角α的始邊與x軸的非負半軸重合,終邊與單位圓交于點A(x1,y1),角β=α+$\frac{2π}{3}$的終邊與單位圓交于點B(x2,y2),記f(α)=y1-y2.若角α為銳角,則f(α)的取值范圍是(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [$\frac{5}{4}$,$\frac{5}{3}$] | B. | [$\frac{3}{2}$,++∞) | C. | (1,4] | D. | [$\frac{3}{2}$,4] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com