
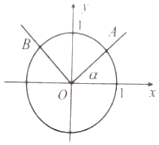
 如圖,角α的始邊與x軸的非負半軸重合,終邊與單位圓交于點A(x1,y1),角β=α+$\frac{2π}{3}$的終邊與單位圓交于點B(x2,y2),記f(α)=y1-y2.若角α為銳角,則f(α)的取值范圍是(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
如圖,角α的始邊與x軸的非負半軸重合,終邊與單位圓交于點A(x1,y1),角β=α+$\frac{2π}{3}$的終邊與單位圓交于點B(x2,y2),記f(α)=y1-y2.若角α為銳角,則f(α)的取值范圍是(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$). 分析 根據三角函數的定義求出函數f(α)的表達式,即可求出處函數的值域.
解答 解:由三角函數定義知,y1=sinα,y2=sin(α+$\frac{2π}{3}$),
f(α)=y1-y2=sinα-sin(α+$\frac{2π}{3}$)=$\frac{3}{2}$sinα-$\frac{\sqrt{3}}{2}$cosα=$\sqrt{3}$sin(α-$\frac{π}{6}$)
∵角α為銳角,
∴-$\frac{π}{6}$<α-$\frac{π}{6}$<$\frac{π}{3}$,
∴-$\frac{1}{2}$<sin(α-$\frac{π}{6}$)<$\frac{\sqrt{3}}{2}$,
∴-$\frac{\sqrt{3}}{2}$<$\sqrt{3}$sin(α-$\frac{π}{6}$)<$\frac{3}{2}$,
則f(α)的取值范圍是(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$),
故答案為(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
點評 本題主要考查三角函數的定義以及三角恒等變換的運用,根據條件求出函數的解析式是解決本題的關鍵.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
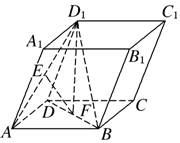 在平行六面體ABCDA1B1C1D1中,設$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,E,F分別是
在平行六面體ABCDA1B1C1D1中,設$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,E,F分別是查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{5}{2}$ | B. | $-\frac{3}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 評估的平均得分 | (0,6) | [6,8) | [8,10] |
| 全市的總體交通狀況等級 | 不合格 | 合格 | 優秀 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com