
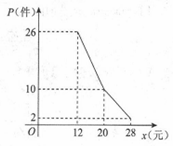
 某網店經營的一種商品進價是每件10元,根據一周的銷售數據得出周銷量P(件)與單價x(元)之間的關系如圖折線所示,該網店與這種商品有關的周開支均為25元.
某網店經營的一種商品進價是每件10元,根據一周的銷售數據得出周銷量P(件)與單價x(元)之間的關系如圖折線所示,該網店與這種商品有關的周開支均為25元.分析 (I)根據函數圖象,求出解析式,即可寫出周銷量P(件)與單價x(元)之間的函數關系式;
(Ⅱ)分段求出最值,即可得出結論.
解答 解:(I)當x∈[12,20]時,P=k1x+b1,代入點(12,26),(20,10)得k1=-2,b1=50,∴P=-2x+50;
同理x∈(20,28]時,P=-x+30,
∴周銷量P(件)與單價x(元)之間的函數關系式P=$\left\{\begin{array}{l}{-2x+50,12≤x≤20}\\{-x+30,20<x≤28}\end{array}\right.$;
(Ⅱ)y=P(x-10)-25=$\left\{\begin{array}{l}{(-2x+50)(x-10)-25,12≤x≤20}\\{(-x+30)(x-10),20<x≤28}\end{array}\right.$,
當x∈[12,20]時,y=$-2(x-\frac{35}{2})^{2}+\frac{175}{2}$,x=$\frac{35}{2}$時,ymax=$\frac{175}{2}$;
x∈(20,28]時,y=-(x-20)2+75,函數單調遞減,∴y<75,
綜上所述,x=$\frac{35}{2}$時,ymax=$\frac{175}{2}$.
點評 本題考查分段函數及運用,考查分段函數的最值,應考慮各段的最值,考查運算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x=$\frac{1}{32}$ | B. | x=$\frac{1}{2}$ | C. | y=2 | D. | y=4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{7}$ | B. | $\frac{4}{3}$ | C. | -$\frac{1}{7}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0個 | B. | 1個 | ||
| C. | 2個 | D. | 不確定,隨k的變化而變化 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0個 | B. | 1個 | ||
| C. | 2個 | D. | 不確定,隨k的變化而變化 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1+|x+y|+|xy|≥|x|+|y| | B. | 1+2|x+y|≥|x|+|y| | C. | 1+2|xy|≥|x|+|y| | D. | |x+y|+2|xy|≥|x|+|y| |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐P-ABCD中,側面PCD⊥底面ABCD,PD⊥CD,E為PC中點,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.
如圖,在四棱錐P-ABCD中,側面PCD⊥底面ABCD,PD⊥CD,E為PC中點,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com