
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 根據題意求出φ與ω的值,寫出f(x)解析式,再求$f(\frac{π}{6})$的值.
解答 解:角φ的終邊在射線$y=\sqrt{3}x(x≤0)$上,
∴φ=-$\frac{2π}{3}$;
又函數f(x)圖象的相鄰兩條對稱軸之間的距離等于$\frac{π}{3}$,
∴T=$\frac{2π}{ω}$=2×$\frac{π}{3}$,
解得ω=3;
∴f(x)=cos(3x-$\frac{2π}{3}$),
∴$f(\frac{π}{6})$=cos(3×$\frac{π}{6}$-$\frac{2π}{3}$)=cos(-$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$.
故選:D.
點評 本題主要考查了任意角的三角函數定義與圖象性質的應用問題,是基礎題.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:高中數學 來源: 題型:解答題
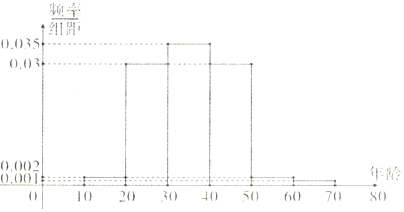
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 110 | B. | 90 | C. | 55 | D. | 45 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p是q的充分不必要條件 | B. | p是q的必要不充分條件 | ||
| C. | p是q的既不充分也不必要條件 | D. | p是q的充要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-2e,e] | B. | [0,2e] | C. | (-∞,-e)∪[e,2e] | D. | (-∞,-e)∪[0,e] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com