
分析 由定義在區間[-2b,3b-1]上的函數f(x)=x3-ax2-(b+2)x是奇函數,列出方程組,能求出a=0,b=1,從而a+b=1,f(x)=x3-3x,由此利用導數的性質能求出函數f(x)的極差.
解答 解:∵定義在區間[-2b,3b-1]上的函數f(x)=x3-ax2-(b+2)x是奇函數,
∴$\left\{\begin{array}{l}{-2b+3b-1=0}\\{-a=0}\end{array}\right.$,解得a=0,b=1,∴a+b=1,
∴f(x)=x3-3x,區間[-2b,3b-1]即為[-2,2].
f′(x)=3x2-3,由f′(x)=0,得x=±1,
∵f(-2)=(-2)3-3×(-2)=-2,
f(-1)=(-1)3-3×(-1)=2,
f(1)=13-3×1=-2,
f(2)=23-3×2=2,
∴f(x)max=2,f(x)min=-2,
∴函數f(x)的極差為:2-(-2)=4.
故答案為:1,4.
點評 本題考查函數性質、函數極差、導數、函數最大值及最小值等基礎知識,考查推理論證能力、運算求解能力、數據處理能力,考查數形結合思想,是中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
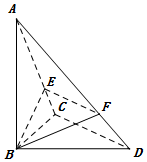 在三棱錐A-BCD中,AB⊥平面BCD,∠BCD=90°,E、F分別是AC、AD上的點,且$\frac{AE}{AC}=\frac{AF}{AD}$.
在三棱錐A-BCD中,AB⊥平面BCD,∠BCD=90°,E、F分別是AC、AD上的點,且$\frac{AE}{AC}=\frac{AF}{AD}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{6}{5}$i | B. | $\frac{8i}{5}$ | C. | -$\frac{8i}{5}$ | D. | -$\frac{6}{5}$i |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,-2) | B. | (-1,2) | C. | (-2,1) | D. | (2,-1) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com