
分析 (1)設g(x)=ax(a>0且a≠1),由a3=8解得a=2.故g(x)=2x.再根據函數是奇函數,求出n的值,得到f(x)的解析式;
(2)根據函數為奇函數和減函數,轉化為即對一切x∈(1,4),有3tx-3<k恒成立,再利用函數的單調性求出函數的最值即可.
解答 解::(1)設g(x)=ax(a>0且a≠1),
∵g(3)=8,∴a3=8,解得a=2.∴g(x)=2x.∴f(x)=$\frac{n-{2}^{x}}{2+2•{2}^{x}}$,
∵函數f(x)是定義域為R的奇函數,∴f(0)=0,∴n=1,∴f(x)=$\frac{1-{2}^{x}}{2+{2}^{x+1}}$,(x∈R);
(2)由(Ⅰ)知f(x)=$-\frac{1}{2}•\frac{{2}^{x}-1}{{2}^{x}+1}=-\frac{1}{2}+\frac{1}{{2}^{x}+1}$,易知f(x)在R上為減函數,
又f(x)是奇函數,∴f(2x-3)+f(x-k)>0,∴f(2x-3)>-f(x-k)=f(k-x),
∵f(x)在R上為減函數,由上式得2x-3<k-x,
即對一切x∈(1,4),有3x-3<k恒成立,
令m(x)=3x-3,x∈(1,4),
易知m(x)在(1,4)上遞增,∴m(x)<3×4-3=9,
∴k≥9,即實數k的取值范圍是[9,+∞).
點評 本題綜合考查了指數函數的定義及其性質、函數的奇偶性、單調性、恒成立問題的等價轉化、屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
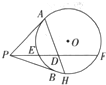 如圖,已知點P是圓O外一點,過P做圓O的切線PA,PB,切點分別為A,B,過P做一條割線交圓O于E,F,若2PA=PF,取PF的中點D,連接AD,并延長交圓于H.
如圖,已知點P是圓O外一點,過P做圓O的切線PA,PB,切點分別為A,B,過P做一條割線交圓O于E,F,若2PA=PF,取PF的中點D,連接AD,并延長交圓于H.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 增函數,最小值-1 | B. | 增函數,最大值-1 | C. | 減函數,最小值-1 | D. | 減函數,最大值-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com