
| A. | $(\frac{1}{3},+∞)$ | B. | $(\frac{1}{3},2)∪(2,+∞)$ | C. | $[\frac{1}{3},2)∪(2,+∞)$ | D. | $[\frac{1}{3},+∞)$ |
分析 根據(jù)函數(shù)成立的條件即可求函數(shù)的定義域.
解答 解:要使函數(shù)有意義,則$\left\{\begin{array}{l}{x>0}\\{1+lo{g}_{3}x≥0}\\{{2}^{x}-4≠0}\end{array}\right.$,
即$\left\{\begin{array}{l}{x>0}\\{lo{g}_{3}x≥-1}\\{x≠2}\end{array}\right.$,即$\left\{\begin{array}{l}{x>0}\\{x≥\frac{1}{3}}\\{x≠2}\end{array}\right.$,即x≥$\frac{1}{3}$且x≠2,
即函數(shù)的定義域為$[\frac{1}{3},2)∪(2,+∞)$,
故選:C
點評 本題主要考查函數(shù)的定義域的求解,要求熟練掌握常見函數(shù)成立的條件.


科目:高中數(shù)學 來源: 題型:選擇題

| A. | $\left\{{\begin{array}{l}{x+y-1≥0}\\{x-2y+2≥0}\\{2x-y-2≤0}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x+y-1≥0}\\{x-2y+2≥0}\\{2x-y-2≥0}\end{array}}\right.$ | ||
| C. | $\left\{{\begin{array}{l}{x+y-1≥0}\\{x-2y+2≤0}\\{2x-y-2≤0}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x+y-1≥0}\\{x-2y+2≤0}\\{2x-y-2≥0}\end{array}}\right.$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
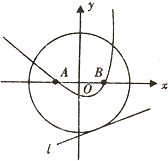 如圖,⊙O:x2+y2=16,A(-2,0),B(2,0)為兩個定點,l是⊙O的一條切線,若過A,B兩點的拋 物線以直線l為準線,則該拋物線的焦點的軌跡是( )
如圖,⊙O:x2+y2=16,A(-2,0),B(2,0)為兩個定點,l是⊙O的一條切線,若過A,B兩點的拋 物線以直線l為準線,則該拋物線的焦點的軌跡是( )| A. | 圓 | B. | 雙曲線 | C. | 橢圓 | D. | 拋物線 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com