
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 確定f(x)的周期為3,函數(shù)在(0,e)上單調(diào)遞增,在(e,3)上單調(diào)遞減,在[0,9]上作出y=f(x)的圖象,作出y=$\frac{x}{6}$的圖象,即可得出結(jié)論.
解答 解:依題意,f′(x)=$\frac{e(1-lnx)}{{x}^{2}}$,故函數(shù)f(x)在上(0,e)單調(diào)遞增,在(e,3)上單調(diào)遞減,
故當(dāng)x∈(0,3)時,f(x)max=f(e)=1,
又函數(shù)f(x)是定義在R上的奇函數(shù),且x>0時,f(-x)+f(x+3)=0,即f(x+3)=f(x),且f(0)=0;
由6f(x)-x=0可知,f(x)=$\frac{x}{6}$.
在同一直角坐標(biāo)系中,作出函數(shù)y=f(x)與y=$\frac{x}{6}$在[-9,9]上的圖象如下圖所示,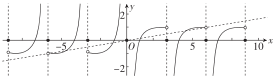
觀察可知,y=f(x)與y=$\frac{x}{6}$有7個交點,即方程6f(x)-x=0的解有7個,
故選D.
點評 本題考查單調(diào)性和極值,函數(shù)的奇偶、周期性,考查學(xué)生分析解決問題的能力,屬于中檔題.


 科學(xué)實驗活動冊系列答案
科學(xué)實驗活動冊系列答案科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 在圓x2+y2=7內(nèi) | B. | 在圓x2+y2=7上 | ||
| C. | 在橢圓$\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{6}$=1內(nèi) | D. | 在橢圓$\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{6}$=1上 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 最小正周期為π | B. | 是奇函數(shù) | ||
| C. | 在區(qū)間$(-\frac{1}{12}π,\frac{5}{12}π)$上單調(diào)遞減 | D. | $(\frac{5}{12}π,0)$為其圖象的一個對稱中心 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
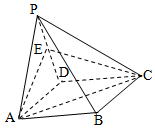 在四棱錐P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中點.
在四棱錐P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中點.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com