
分析 依題意,f由(x+a)≤f(x)對任意的x∈R恒成立,在同一坐標系中作出滿足題意的y=f(x+a)與y=f(x)的圖象,可得x(1+ax)+1≥(x+a)[1-a(x+a)]+1恒成立,整理后為二次不等式,利用△≤0即可求得實數a的取值范圍.
解答 解:∵f(x)=x(1-a|x|)+1=$\left\{\begin{array}{l}{x(1+ax)+1,x<0}\\{x(1-ax)+1,x≥0}\end{array}\right.$=$\left\{\begin{array}{l}{{a(x+\frac{1}{2a})}^{2}+1-\frac{1}{4a},x<0}\\{-{a(x-\frac{1}{2a})}^{2}+1+\frac{1}{4a},x≥0}\end{array}\right.$(a>0),
∴f(x+a)=(x+a)(1-a|x+a|)+1,
∵f(x+a)≤f(x)對任意的x∈R恒成立,
在同一坐標系中作出滿足題意的y=f(x+a)與y=f(x)的圖象如下: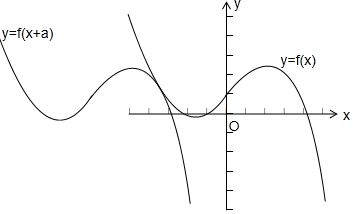
∴x(1+ax)+1≥(x+a)[1-a(x+a)]+1恒成立,
即x+ax2+1≥-a(x2+2ax+a2)+x+a+1,
整理得:2x2+2ax+a2-1≥0恒成立,
∴△=4a2-4×2(a2-1)≤0,
解得:a≥$\sqrt{2}$.
故答案為:[$\sqrt{2}$,+∞).
點評 本題考查函數恒成立問題,深刻理解f(x+a)≤f(x)對任意的x∈R恒成立,得到x(1+ax)+1≥(x+a)[1-a(x+a)]+1恒成立是解決問題的關鍵,也是難點,考查作圖、分析與運算能力,屬于難題.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,0) | B. | (-∞,-3) | C. | (3,+∞) | D. | (-3,0) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
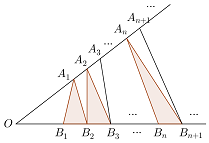 如圖,點列{An}、{Bn}分別在銳角兩邊(不在銳角頂點),且|AnAn+1|=|An+1An+2|,An≠An+2,|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+1,n∈N*(P≠Q表示點P與Q不重合),若dn=|AnBn|,Sn為△AnBnBn+1的面積,則( )
如圖,點列{An}、{Bn}分別在銳角兩邊(不在銳角頂點),且|AnAn+1|=|An+1An+2|,An≠An+2,|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+1,n∈N*(P≠Q表示點P與Q不重合),若dn=|AnBn|,Sn為△AnBnBn+1的面積,則( )| A. | {dn}是等差數列 | B. | {Sn}是等差數列 | ||
| C. | {d${\;}_{n}^{2}$}是等差數列 | D. | {S${\;}_{n}^{2}$}是等差數列 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{{π^2}+4}$ | B. | $2\sqrt{{π^2}+1}$ | C. | $\sqrt{\frac{π^2}{4}+4}$ | D. | $\sqrt{\frac{π^2}{16}+4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com