
| A. | -$\sqrt{6}$ | B. | -$\frac{\sqrt{6}}{2}$ | C. | ±$\sqrt{6}$ | D. | ±$\frac{\sqrt{6}}{2}$ |
分析 利用二倍角公式化簡,再利用正弦函數的定義,建立方程,即可得出結論.
解答 解:2sin2$\frac{π}{8}$-1=-cos$\frac{π}{4}$=-$\frac{\sqrt{2}}{2}$,2$\sqrt{3}$sin$\frac{13π}{12}$cos$\frac{π}{12}$=-$\frac{\sqrt{3}}{2}$,
∵角θ的終邊過點(2sin2$\frac{π}{8}$-1,a),sinθ=2$\sqrt{3}$sin$\frac{13π}{12}$cos$\frac{π}{12}$,
∴$\frac{a}{\sqrt{\frac{1}{2}+{a}^{2}}}$=-$\frac{\sqrt{3}}{2}$,
∴a=-$\frac{\sqrt{6}}{2}$,
故選B.
點評 本題考查正弦函數的定義,考查二倍角公式,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{9}{2}$ | B. | $\frac{9}{2}$ | C. | $\frac{1}{4}$ | D. | -4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {-3,-2,-1} | B. | {-1,2,3} | C. | {-1,0,1,2,3} | D. | {0,1} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {m|m<-2或m>2} | B. | {m|-2<m<2} | C. | {m|m<0或m>4} | D. | {m|0<m<4} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 命題“?x0∈R,x02-x0≤0”的否定為“?x∈R,x2-x>0” | |
| B. | 若非零向量$\overrightarrow a$、$\overrightarrow b$滿足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,則$\overrightarrow a$與$\overrightarrow b$共線 | |
| C. | 命題“在△ABC中,A>30°,則sinA>$\frac{1}{2}$”的逆否命題為真命題 | |
| D. | 設{an}是公比為q的等比數列,則“q>1”是“{an}為遞增數列”的充分必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
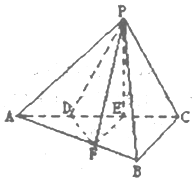 如圖,三棱錐P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,點D、E在線段AC上,且AD=DE=EC=1,PD=PC=2,點F在線段AB上,且EF∥BC.
如圖,三棱錐P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,點D、E在線段AC上,且AD=DE=EC=1,PD=PC=2,點F在線段AB上,且EF∥BC.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com