
分析 由約束條件作出可行域,再由z=$\frac{2x+y}{\sqrt{{x}^{2}+{y}^{2}}}$的幾何意義,即向量$\overrightarrow{OA}$與向量$\overrightarrow{OP}$夾角的余弦值的$\sqrt{5}$倍求解.
解答 解:由約束條件$\left\{\begin{array}{l}{x-2y≥0}\\{x-y-1≤0}\\{y>0}\end{array}\right.$作出可行域如圖,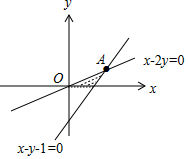
設A(2,1),可行域內的動點P(x,y),
則cos<$\overrightarrow{OA},\overrightarrow{OP}$>=$\frac{2x+y}{\sqrt{{x}^{2}+{y}^{2}}•\sqrt{5}}$.
z=$\frac{2x+y}{\sqrt{{x}^{2}+{y}^{2}}}$=$\sqrt{5}•\frac{2x+y}{\sqrt{{x}^{2}+{y}^{2}}•\sqrt{5}}$.
其幾何意義為向量$\overrightarrow{OA}$與向量$\overrightarrow{OP}$夾角的余弦值的$\sqrt{5}$倍,
∴當P與A重合時,z=$\frac{2x+y}{\sqrt{{x}^{2}+{y}^{2}}}$有最大值為$\sqrt{5}$.
故答案為:$\sqrt{5}$.
點評 本題考查簡單的線性規劃,考查了數形結合的解題思想方法與數學轉化思想方法,是難題.


 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南師范大學出版社系列答案
同步練習西南師范大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
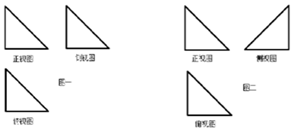 小明在解決三視圖還原問題時,錯把圖一的三視圖看成圖二的三視圖,假設圖一所對應幾何體中最大的面積為S1,圖二所對應幾何體中最大面的面積為S2,三視圖中所有三角形均為全等的等腰直角三角形,則$\frac{{S}_{1}}{{S}_{2}}$=( )
小明在解決三視圖還原問題時,錯把圖一的三視圖看成圖二的三視圖,假設圖一所對應幾何體中最大的面積為S1,圖二所對應幾何體中最大面的面積為S2,三視圖中所有三角形均為全等的等腰直角三角形,則$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | 1 | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①②③ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\sqrt{6}$ | B. | -$\frac{\sqrt{6}}{2}$ | C. | ±$\sqrt{6}$ | D. | ±$\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 40 | B. | 20 | C. | 31 | D. | 43 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com