
分析 方法一:將被積函數裂項,根據定積分的運算,即可求得答案.
方法二:化簡,$∫\underset{\stackrel{2}{\;}}{1}\frac{dx}{{x}^{2}-2x-3}$=${∫}_{1}^{2}$$\frac{d(x-1)}{(x-1)^{2}-{2}^{2}}$,利用不定積分公式,求得原函數,代入即可求得答案.
解答 解:方法一:$∫\underset{\stackrel{2}{\;}}{1}\frac{dx}{{x}^{2}-2x-3}$=${∫}_{1}^{2}$$\frac{1}{(x+1)(x-3)}$dx=${∫}_{1}^{2}$$\frac{1}{4}$($\frac{1}{x-3}$-$\frac{1}{x+1}$)dx=$\frac{1}{4}$(${∫}_{1}^{2}$$\frac{1}{x-3}$dx-${∫}_{1}^{2}$$\frac{1}{x+1}$dx)=$\frac{1}{4}$[${∫}_{1}^{2}$$\frac{1}{3-x}$d(3-x)-${∫}_{1}^{2}$$\frac{1}{x+1}$d(x+1)],
=$\frac{1}{4}$[ln(3-x)${丨}_{1}^{2}$-ln(x+1)${丨}_{1}^{2}$]=$\frac{1}{4}$[ln(3-2)-ln(3-1)-ln(2+1)+ln(1+1)],
=-$\frac{ln3}{4}$,
∴$∫\underset{\stackrel{2}{\;}}{1}\frac{dx}{{x}^{2}-2x-3}$=-$\frac{ln3}{4}$,
方法二:$∫\underset{\stackrel{2}{\;}}{1}\frac{dx}{{x}^{2}-2x-3}$=${∫}_{1}^{2}$$\frac{1}{(x-1)^{2}-4}$dx=${∫}_{1}^{2}$$\frac{1}{(x-1)^{2}-4}$dx=${∫}_{1}^{2}$$\frac{d(x-1)}{(x-1)^{2}-4}$=${∫}_{1}^{2}$$\frac{d(x-1)}{(x-1)^{2}-{2}^{2}}$=($\frac{1}{4}$ln丨$\frac{2-(x-1)}{2+(x-1)}$丨)${丨}_{1}^{2}$=($\frac{1}{4}$ln丨$\frac{3-x}{1+x}$丨)${丨}_{1}^{2}$=$\frac{1}{4}$(-ln3-ln1)=-$\frac{ln3}{4}$,
∴$∫\underset{\stackrel{2}{\;}}{1}\frac{dx}{{x}^{2}-2x-3}$=-$\frac{ln3}{4}$,
利用不定積分∫$\frac{dx}{{x}^{2}-{a}^{2}}$=$\frac{1}{2a}$ln丨$\frac{a-x}{a+x}$丨+C,
點評 本題考查定積分的計算,考查求原函數的方程,考查求原函數的公式,考查裂項法被奇函數的原函數,是大學高數的方法,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
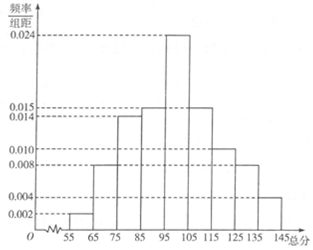 某省組織了一次高考模擬考試,該省教育部門抽取了1000名考生的數學考試成績,并繪制成頻率分布直方圖如圖所示.
某省組織了一次高考模擬考試,該省教育部門抽取了1000名考生的數學考試成績,并繪制成頻率分布直方圖如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 90 | B. | 45 | C. | 120 | D. | 180 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com