Question

8．已知函數f（x）=$\left\{\begin{array}{l}{（\frac{1}{2}）^{x}-1，x≤0}\\{2{x}^{2}-lnx，x＞0}\end{array}\right.$，若函數y=f（x）-a恰有一個零點，則a的取值范圍是[0，$\frac{1}{2}$-ln$\frac{1}{2}$）．

Answer 1

分析 判斷f（x）的單調性，作出f（x）的函數圖象，根據函數圖象得出a的范圍．

解答 解：當x＞0時，f′（x）=4x-$\frac{1}{x}$=$\frac{4{x}^{2}-1}{x}$，
∴當0$＜x＜\frac{1}{2}$時，f′（x）＜0，當x$＞\frac{1}{2}$時，f′（x）＞0，
∴f（x）在（0，$\frac{1}{2}$）上單調遞減，在（$\frac{1}{2}$，+∞）上單調遞增，
∴當x=$\frac{1}{2}$時，f（x）取得極小值f（$\frac{1}{2}$）=$\frac{1}{2}$-ln$\frac{1}{2}$，
作出f（x）的函數圖象，如圖所示：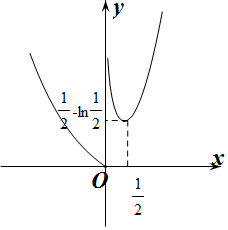

∵函數y=f（x）-a恰有一個零點，
∴0≤a＜$\frac{1}{2}-$ln$\frac{1}{2}$．
故答案為：[0，$\frac{1}{2}-$ln$\frac{1}{2}$）．

點評 本題考查了函數零點與函數圖象的關系，函數單調性的判斷與極值計算，屬于中檔題．