
分析 (1)當a=-$\frac{1}{3}$時,求導,令f′(x)=0,解得x=3,令f′(x)>0,求得f(x)在區間[e,3)上單調遞增,令f′(x)<0,f(x)在區間(3,e2]上單調遞減,可得函數f(x)在x=3時取極大值;
(2)當a=1時,求得g(x)的解析式,由題意可知:f(x)-$\frac{2}{t}$x2=0只有一個實數解,即2x2-tlnx-tx=0只有唯一正實數解,設h(x)=2x2-tlnx-tx,求導,令h′(x)=0,求得x2=$\frac{t+\sqrt{{t}^{2}+16t}}{8}$,根據函數的單調性可知:h(x)的最小值h(x2),因此2lnx2+x2-1=0,設m(x)=2lnx+x-1(x>0),求導m′(x)=$\frac{2}{x}$+1>0恒成立,m(x)=0至多有一解,由m(1)=0,則x2=1,即$\frac{t+\sqrt{{t}^{2}+16t}}{8}$=1,即可求得t的值.
解答 解:(1)當a=-$\frac{1}{3}$時,求導f′(x)=$\frac{1}{x}$-$\frac{1}{3}$=$\frac{3-x}{3x}$(x∈[e,e2]),…(1分)
由f′(x)=0,解得x=3,
當x∈[e,3)時,f′(x)>0,f(x)在區間[e,3)上單調遞增,
當x∈(3,e2]時,f′(x)<0,f(x)在區間(3,e2]上單調遞減,…(3分)
∴f(x)在區間[e,e2]上只有極大值,無極小值,且f(x)極大值=f(3)=ln3-1,…(5分)
(2)當a=1時,g(x)=f(x)-$\frac{2}{t}$x2,只有一個零點,等價于方程f(x)-$\frac{2}{t}$x2=0只有一個實數解,
即2x2-tlnx-tx=0只有唯一正實數解.
設h(x)=2x2-tlnx-tx,則h′(x)=4x-$\frac{t}{x}$-t=$\frac{4{x}^{2}-tx-t}{x}$,
令h′(x)=0,即4x2-tx-t=0,
∵x>0,t>0,
解得:x1=$\frac{t-\sqrt{{t}^{2}+16t}}{8}$,x2=$\frac{t+\sqrt{{t}^{2}+16t}}{8}$,…(7分)
當x∈(0,x2)時,h′(x)<0,則h(x)在(0,x2)上單調遞減;
當x∈(x2,+∞)時,h′(x)>0,則h(x)在(x2,+∞)上單調遞增;
∴h(x)的最小值h(x2),…(8分)
要使得方程2x2-tlnx-tx=0只有唯一實數解,
則$\left\{\begin{array}{l}{h({x}_{2})=0}\\{h′({x}_{2})=0}\end{array}\right.$,即$\left\{\begin{array}{l}{2{x}_{2}^{2}-tln{x}_{2}-t{x}_{2}=0}\\{4{x}_{2}^{2}-t{x}_{2}-t=0}\end{array}\right.$,得
2tlnx2+tx2-t=0,
∵t>0,
∴2lnx2+x2-1=0,…(10分)
設m(x)=2lnx+x-1(x>0),求導m′(x)=$\frac{2}{x}$+1>0恒成立,
故m(x)在(0,+∞)單調遞增,
m(x)=0至多有一解,
又∵m(1)=0,
∴x2=1,即$\frac{t+\sqrt{{t}^{2}+16t}}{8}$=1,
解得:t=2,
正數t的值2.…(12分)
點評 本題考查函數的導數,極值,最值及單調性,考查利用導數研究函數的單調性及最值,考查構造法求函數的最值,考查計算能力,屬于難題.


 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案科目:高中數學 來源: 題型:解答題
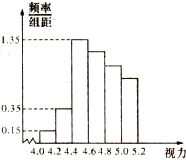 某學校研究性學習小組對該校高三學生視力情況進行調查,在髙三的全體1000名學生中隨機抽取了100名學生的體檢表,并得到如圖的頻率分布直方圖.
某學校研究性學習小組對該校高三學生視力情況進行調查,在髙三的全體1000名學生中隨機抽取了100名學生的體檢表,并得到如圖的頻率分布直方圖.| 年級名次 是否近視 | 1~50 | 951~1000 |
| 近視 | 41 | 32 |
| 不近視 | 9 | 18 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | lna>-b-1 | B. | lna≥-b-1 | C. | lna<-b-1 | D. | lna≤-b-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | -3 | C. | $-2\sqrt{3}$ | D. | -2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com