
分析 根據函數奇偶性和單調性之間的關系將不等式等價轉化為x>0時f(x-1)>f(2),x<0時,f(x-1)<f(-2),即可得到結論.
解答 解:∵偶函數f(x)在[0,+∞)單調遞減,f(2)=0,
∴f(x)在(-∞,0)遞增,f(-2)=0;
∴x>0時,不等式xf(x-1)>0等價為f(x-1)>f(2),
即x-1<2,解得:0<x<3;
x<0時:不等式xf(x-1)>0等價為f(x-1)<f(-2),
即x-1<-2,解得:x<-1,
故答案為:(-∞,-1)∪(0,3).
點評 本題主要考查函數奇偶性和單調性之間的關系的應用,將不等式等價轉化為f(x-1)>f(2)或f(x-1)<f(-2)是解決本題的關鍵.


 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 10個 | B. | 9個 | C. | 8個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
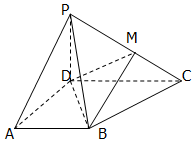 如圖,四棱錐P-ABCD中,底面ABCD為梯形,∠DAB=60°,AB∥CD,AD=CD=2AB=2,PD⊥底面ABCD,M為PC的中點.
如圖,四棱錐P-ABCD中,底面ABCD為梯形,∠DAB=60°,AB∥CD,AD=CD=2AB=2,PD⊥底面ABCD,M為PC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
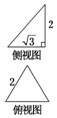 已知三棱錐的俯視圖與側視圖如圖所示,俯視圖是邊長為2的正三角形,側視圖是有一條直角邊為2的直角三角形,則該三棱錐的正視圖可能為( )
已知三棱錐的俯視圖與側視圖如圖所示,俯視圖是邊長為2的正三角形,側視圖是有一條直角邊為2的直角三角形,則該三棱錐的正視圖可能為( )| A. | 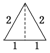 | B. |  | C. | 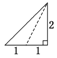 | D. | 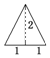 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com