
分析 (1)根據題意,由函數奇偶性的性質可得f(0)=0,即1+k-1+k2=0,解得k=0或k=1,驗證k=1和k=0時,f(x)是不是奇函數,即可得答案;
(2)根據題意,由于f(1)>0,可得a2-1>0,a>1,分析可得f(x)在R上為增函數,結合單調性的性質可得f(x2+x)>f(2x-t)恒成立,變形可得t>-x2+x恒成立,結合二次函數的性質,分析-x2+x的最大值,即可得實數t的取值范圍;
(3)由f(1)=$\frac{3}{2}$分析可得$f(1)=a-\frac{1}{a}=\frac{3}{2}$,結合a>0解得a的值,則g(x)的解析式,利用還原法分析可得答案.
解答 解:(1)因為f(x)是定義域為R的奇函數,
所以f(0)=0,即1+k-1+k2=0,解得k=0或k=1,
當k=1時,顯然f(x)不是奇函數;
當k=0時,f(x)=ax-a-x,滿足f(-x)+f(x)=0,
f(x)是奇函數,所以k=0.
(2)因為$f(1)=a-\frac{1}{a}>0$,a>0,所以a2-1>0,a>1,f(x)在R上為增函數,
由f(x2+x)+f(t-2x)>0,得f(x2+x)>f(2x-t),即x2+x>2x-t,即t>-x2+x恒成立,
又因為-x2+x的最大值為$\frac{1}{4}$,所以$t>\frac{1}{4}$.
所以實數t的取值范圍是$(\frac{1}{4},+∞)$.
(3)由$f(1)=a-\frac{1}{a}=\frac{3}{2}$,解得a=2或$a=-\frac{1}{2}$,
又a>0,所以a=2,
則g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2,
設u=2x-2-x,當x∈[1,+∞)時,$u∈[\frac{3}{2},+∞)$,y=u2-2mu+2在$u∈[\frac{3}{2},+∞)$上的最小值為-1.
所以$\left\{\begin{array}{l}m≤\frac{3}{2}\\ \frac{9}{4}-3m+2=-1\end{array}\right.$或$\left\{\begin{array}{l}m>\frac{3}{2}\\-{m^2}+2=-1\end{array}\right.$,解得$m=\sqrt{3}$.
點評 本題考查函數的恒成立問題,涉及函數奇偶性與單調性的綜合運用,注意恒成立問題的轉化.


 孟建平錯題本系列答案
孟建平錯題本系列答案 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{3}-1}}{2}$ | B. | $\sqrt{3}-1$ | C. | $\frac{{\sqrt{3}-\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}+1}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
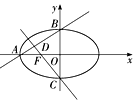 如圖所示,橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率e=$\frac{1}{2}$,左焦點為F,A、B、C為其三個頂點,直線CF與AB交于D點,則tan∠ADF的值等于( )
如圖所示,橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率e=$\frac{1}{2}$,左焦點為F,A、B、C為其三個頂點,直線CF與AB交于D點,則tan∠ADF的值等于( )| A. | 3$\sqrt{3}$ | B. | -3$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{5}$ | D. | -$\frac{\sqrt{3}}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
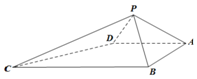 如圖,四棱錐P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等邊三角形,則直線PC與平面ABCD所成角的正切值為( )
如圖,四棱錐P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等邊三角形,則直線PC與平面ABCD所成角的正切值為( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com