Question

9．等腰直角三角形ABC中，AB=AC=4，且2$\overrightarrow{AE}$=$\overrightarrow{EC}$，$\overrightarrow{BD}$=$\overrightarrow{DC}$，則$\overrightarrow{BE}$•$\overrightarrow{AD}$=-$\frac{16}{3}$．

Answer 1

分析 求得$\overrightarrow{AB}$•$\overrightarrow{AC}$=0，由中點向量表示和向量共線，$\overrightarrow{BE}$、$\overrightarrow{AD}$統一成$\overrightarrow{AB}$、$\overrightarrow{AC}$表示，再由向量數量積的性質：向量的平方即為模的平方，計算即可得到所求值．

解答 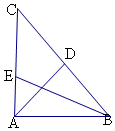解：$\overrightarrow{AB}$•$\overrightarrow{AC}$=4×4×cos90°=0，
2$\overrightarrow{AE}$=$\overrightarrow{EC}$，$\overrightarrow{BD}$=$\overrightarrow{DC}$，
則$\overrightarrow{BE}$•$\overrightarrow{AD}$=（$\overrightarrow{AE}$-$\overrightarrow{AB}$）•$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$）
=（$\frac{1}{3}$$\overrightarrow{AC}$-$\overrightarrow{AB}$）•$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$）
=$\frac{1}{6}$$\overrightarrow{AC}$²-$\frac{1}{2}$$\overrightarrow{AB}$²-$\frac{1}{3}$$\overrightarrow{AB}$•$\overrightarrow{AC}$
=$\frac{1}{6}$×16-$\frac{1}{2}$×16=-$\frac{16}{3}$．
故答案為：-$\frac{16}{3}$．

點評 本題考查向量數量積的定義和性質，主要是向量的平方即為模的平方，以及中點向量表示，向量共線等，考查運算能力，屬于中檔題．