Question

3．已知以點$C（t，\frac{2}{t}）$（t∈R，t≠0）為圓心的圓與x軸交點為O、A，與y軸交于點O、B，其中O為坐標原點．
（1）試寫出圓C的標準方程，并證明△OAB的面積為定值；
（2）設直線y=-2x+4與圓C交于點M，N，若|OM|=|ON|，求圓C的標準方程．

Answer 1

分析 （1）由已知求出圓的半徑，得到圓的方程，求出A，B的坐標，代入三角形面積公式得答案；
（2）由|OM|=|ON|，可得OC垂直平分線段MN，求出直線OC的方程，得到OC的斜率，利用斜率的關系求得t值，可得圓C的標準方程．

解答 解：（1）∵圓C過原點O，∴$O{C^2}={t^2}+\frac{4}{t^2}$，即圓C標準方程為${（x-t）^2}+{（y-\frac{2}{t}）^2}={t^2}+\frac{4}{t^2}$．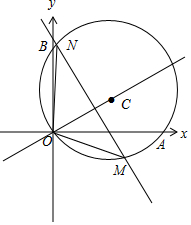
令x=0，得y₁=0，${y_2}=\frac{4}{t}$；令y=0，得x₁=0，x₂=2t．
∴${S_{△OAB}}=\frac{1}{2}OA•OB=\frac{1}{2}|{\frac{4}{t}}|•|{2t}|=4$，即△OAB的面積為定值4；
（2）∵|OM|=|ON|，∴OC垂直平分線段MN，直線OC的方程為$y=\frac{1}{2}x$，
即$\frac{2}{t}=\frac{1}{2}t$，得t=2或t=-2．
當t=2時，滿足題意；當t=-2時，直線y=-2x+4與圓C不相交，舍去．
∴圓C的標準方程為（x-2）²+（y-1）²=5．

點評 本題考查圓的標準方程，考查直線與圓位置關系的應用，考查兩直線垂直與斜率的關系，是中檔題．