
分析 (1)設出M,P的坐標,由向量等式把P的坐標用M的坐標表示,代入橢圓方程整理可得點M的軌跡E的方程;
(2)寫出直線AB的截距式方程,再設出與直線AB平行的直線l的方程為x-y+m=0,與橢圓方程聯立,利用判別式等于0求得m值,結合三角形面積公式得答案.
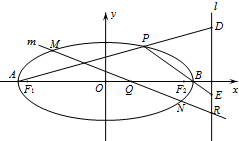
解答 解:(1)設M(x,y),P(x0,y0),
由$\overrightarrow{OM}=\frac{1}{3}\overrightarrow{OP}$,得$({x,y})=\frac{1}{3}({{x_0},{y_0}})⇒\left\{\begin{array}{l}{x_0}=3x\\{y_0}=3y\end{array}\right.$,
∵P(x0,y0)在橢圓上,
∴$\frac{{{x_0}^2}}{36}+\frac{{{y_0}^2}}{9}=1$,即$\frac{9{x}^{2}}{36}+\frac{9{y}^{2}}{9}=1$,則$\frac{x^2}{4}+{y^2}=1$,
∴點M的軌跡E的方程為$\frac{x^2}{4}+{y^2}=1$;
(2)由題意可得直線AB的方程為x-y+4=0,
設與直線AB平行的直線l的方程為x-y+m=0,
由$\left\{{\begin{array}{l}{x-y+m=0}\\{\frac{x^2}{4}+{y^2}=1}\end{array}}\right.$,得5x2+8mx+4m2-4=0.
令△=0,得64m2-4×5×(4m2-4)=0,解得$m=±\frac{5}{4}$,
∵△ABC的面積$S=\frac{1}{2}\sqrt{{4^2}+{4^2}}\frac{{|{m-4}|}}{{\sqrt{2}}}=2|{m-4}|$,
∴當$m=-\frac{5}{4}$時,△ABC的面積有最大值為$\frac{21}{2}$.
點評 本題考查橢圓的簡單性質,考查了直線與橢圓位置關系的應用,是中檔題.


科目:高中數學 來源: 題型:選擇題
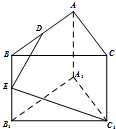 在正三棱柱ABC-A1B1C1中,AB=2,點D、E分別是棱AB、BB1的中點,若DE⊥EC1,則側棱AA1的長為( )
在正三棱柱ABC-A1B1C1中,AB=2,點D、E分別是棱AB、BB1的中點,若DE⊥EC1,則側棱AA1的長為( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 橢圓C的方程為$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分別是它的左、右焦點,已知橢圓C過點(0,1),且離心率e=$\frac{2\sqrt{2}}{3}$.
橢圓C的方程為$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分別是它的左、右焦點,已知橢圓C過點(0,1),且離心率e=$\frac{2\sqrt{2}}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com