
分析 求出函數的導數,可得曲線在x=2處切線的斜率,求得切點,運用點斜式方程,再由y=0,可得交點A.
解答 解:f(x)=$\frac{x}{{{e^{2x}}}}$的導數為f′(x)=$\frac{{e}^{2x}-2x{e}^{2x}}{({e}^{2x})^{2}}$=$\frac{1-2x}{{e}^{2x}}$,
可得曲線f(x)=$\frac{x}{{{e^{2x}}}}$在x=2處的切線斜率為f′(2)=$\frac{-3}{{e}^{4}}$,
切點為(2,$\frac{2}{{e}^{4}}$),
則曲線f(x)=$\frac{x}{{{e^{2x}}}}$在x=2處的切線方程為y-$\frac{2}{{e}^{4}}$=$\frac{-3}{{e}^{4}}$(x-2),
可令y=0,則x=$\frac{8}{3}$.
即有切線與x軸交點A的坐標為($\frac{8}{3}$,0).
點評 本題考查導數的運用:求切線方程,注意運用導數的運算法則和直線的點斜式方程,考查運算能力,屬于基礎題.


 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|x≤-1} | B. | {x|x≥3} | C. | {x|x≤-1或x≥3} | D. | {x|x≤0或x≥3} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
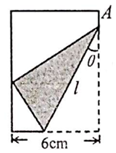 如圖,將矩形紙片的右下角折起,使得該角的頂點落在矩形的左邊上,若$sinθ=\frac{1}{4}$,則折痕l的長度=$\frac{64}{5}$cm.
如圖,將矩形紙片的右下角折起,使得該角的頂點落在矩形的左邊上,若$sinθ=\frac{1}{4}$,則折痕l的長度=$\frac{64}{5}$cm.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
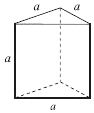
| A. | a2 | B. | $\frac{{\sqrt{3}}}{2}{a^2}$ | C. | $\sqrt{3}{a^2}$ | D. | $\frac{{\sqrt{3}}}{4}{a^2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com