
分析 (1)設$\overrightarrow{a}$=(x,y),推出x2+y2=5,通過$\overrightarrow{a}$∥$\overrightarrow{b}$,即可求解$\overrightarrow{a}$的坐標.
(2)因為$\overrightarrow{a}$-$\overrightarrow{b}$與5$\overrightarrow{a}$+2$\overrightarrow{b}$垂直,數量積為0,得到5$\overrightarrow{a}$2-3$\overrightarrow{a}$•$\overrightarrow{b}$-2$\overrightarrow{b}$2=0,求出$\overrightarrow{a}$•$\overrightarrow{b}$=-5,利用數量積求解cosθ,然后θ∈[0,π],求出$θ=\frac{2π}{3}$.
解答 解:(1)設$\overrightarrow{a}$=(x,y),則x2+y2=5…(2分)
因為$\overrightarrow{a}$∥$\overrightarrow{b}$,所以4y-2x=0…(4分)
由$\left\{\begin{array}{l}{x^2}+{y^2}=5\\ 4y-2x=0\end{array}\right.$,可得$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$或$\left\{\begin{array}{l}x=-2\\ y=-1\end{array}\right.$
所以$\overrightarrow{a}$的坐標為:(2,1)或(-2,-1);…(6分)
(2)因為$\overrightarrow{a}$-$\overrightarrow{b}$與5$\overrightarrow{a}$+2$\overrightarrow{b}$垂直,所以($\overrightarrow{a}$-$\overrightarrow{b}$)(5$\overrightarrow{a}$+2$\overrightarrow{b}$)=0…(8分)
化簡得:5$\overrightarrow{a}$2-3$\overrightarrow{a}$•$\overrightarrow{b}$-2$\overrightarrow{b}$2=0
又因為$|\overrightarrow{a}|=\sqrt{5}$,$|\overrightarrow{b}|=2\sqrt{5}$,所以$\overrightarrow{a}$•$\overrightarrow{b}$=-5…(10分)
cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{-5}{\sqrt{5}•2\sqrt{5}}=-\frac{1}{2}$…(12分)
又因為θ∈[0,π],所以$θ=\frac{2π}{3}$. …(14分)
點評 本題考查向量的數量積的應用,向量共線以及坐標運算,考查計算能力.


 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 5 | D. | 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{28}{75}$ | B. | $\frac{28}{75}$ | C. | -$\frac{56}{75}$ | D. | $\frac{56}{75}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
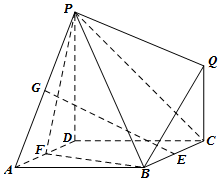 如圖所示的多面體中,面ABCD是邊長為2的正方形,平面PDCQ⊥平面ABCD,PD⊥DC,E,F,G分別為棱BC,AD,PA的中點.
如圖所示的多面體中,面ABCD是邊長為2的正方形,平面PDCQ⊥平面ABCD,PD⊥DC,E,F,G分別為棱BC,AD,PA的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com