Question

14．長方體ABCD-A₁B₁C₁D₁中，$A{A_1}=\sqrt{2}$，AB=1，AD=2，E為BC的中點．設△A₁DE的重心為G，問是否存在實數λ，使得$\overrightarrow{AM}=λ\overrightarrow{AD}$，且MG⊥平面A₁DE同時成立？若存在，求出λ的值；若不存在，說明理由．

Answer 1

分析 過G作GM∥AH交AD于M，由AH⊥面A₁DE得到MG⊥面A₁DE，再利用重心的性質及平行線截線段成比例定理得到λ的值．

解答 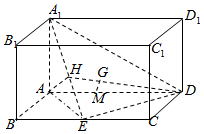解：存在實數$λ=\frac{1}{3}$，使得$\overrightarrow{AM}=λ\overrightarrow{AD}$，
且MG⊥平面A₁DE同時成立
理由如下：由題意求得AE=$\sqrt{2}$，DE=$\sqrt{2}$，
又AD=2，∴AE²+ED²=AD²，∴AE⊥DE．
又DE⊥AA₁，AA₁∩AE=A，AA₁?面A₁AE，
AE?面A₁AE，
∴DE⊥面A₁AE，∴平面A₁AE⊥平面A₁ED，
∵AA₁=AE=$\sqrt{2}$，
取A₁E的中點H，AH⊥A₁E，AH⊥DE，A₁E∩ED=E，A₁E?面A₁DE，
 ED?面A₁DE，∴AH⊥面A₁DE，
在三角形A₁ED中，∵H是A₁E的中點，G為三角形A₁ED的重心，
又∵AH⊥面A₁ED，過點G作GM∥AH交AD于M，
則MG⊥A₁ED，且AM=$\frac{1}{3}AD$，
故存在實數$λ=\frac{1}{3}$，使得$\overrightarrow{AM}=λ\overrightarrow{AD}$，且MG⊥平面A₁DE同時成立．

點評 本題考查了直線與平面平行的判定定理的應用，考查空間想象能力以及邏輯推理能力、轉化思想的應用．屬于中檔題．