
分析 (1)設M(x,y),$x≥\sqrt{2}$,左焦點${F_1}(-\sqrt{5},0)$,通過$\overrightarrow{OM}•\overrightarrow{{F_1}M}=(x,y)•(x+\sqrt{5},y)$利用二次函數的性質求出對稱軸$x=-\frac{{\sqrt{5}}}{5}≤\sqrt{2}$,求出$\overrightarrow{OM}•\overrightarrow{{F_1}M}$的取值范圍.
(2)寫出P點軌跡為橢圓$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,利用$|{{F_1}{F_2}}|=2\sqrt{5}$,|PF1|+|PF2|=2a,結合余弦定理,以及基本不等式求解橢圓方程即可.
解答 解:(1)設M(x,y),$x≥\sqrt{2}$,左焦點${F_1}(-\sqrt{5},0)$,$\overrightarrow{OM}•\overrightarrow{{F_1}M}=(x,y)•(x+\sqrt{5},y)$=${x^2}+\sqrt{5}x+{y^2}={x^2}+\sqrt{5}x+\frac{{3{x^2}}}{2}-3$…(4分)
=$\frac{5}{2}{x^2}+\sqrt{5}x-3$($x≥\sqrt{2}$)
對稱軸$x=-\frac{{\sqrt{5}}}{5}≤\sqrt{2}$,
$\overrightarrow{OM}•\overrightarrow{{F_1}M}∈[{2+\sqrt{10},+∞})$…(3分)
(2)由橢圓定義得:P點軌跡為橢圓$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,$|{{F_1}{F_2}}|=2\sqrt{5}$,|PF1|+|PF2|=2a$cos∠{F_1}P{F_2}=\frac{{{{|{P{F_1}}|}^2}+{{|{P{F_2}}|}^2}-20}}{{2|{P{F_1}}|•|{P{F_2}}|}}=\frac{{4{a^2}-2|{P{F_1}}|•|{P{F_2}}|-20}}{{2|{P{F_1}}|•|{P{F_2}}|}}$=$\frac{{4{a^2}-20}}{{2|{P{F_1}}|•|{P{F_2}}|}}-1$…(4分)
由基本不等式得$2a=|{P{F_1}}|+|{P{F_2}}|≥2\sqrt{|{P{F_1}}|•|{P{F_2}}|}$,
當且僅當|PF1|=|PF2|時等號成立$|{P{F_1}}|•|{P{F_2}}|≤{a^2}$$⇒cos∠{F_1}P{F_2}≥\frac{{4{a^2}-20}}{{2{a^2}}}-1=-\frac{1}{9}⇒{a^2}=9$,b2=4
所求動點P的軌跡方程為$\frac{x^2}{9}+\frac{y^2}{4}=1$…(3分)
點評 本題考查直線與橢圓的位置關系的應用,橢圓方程的求法,考查計算能力.


 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:高中數學 來源: 題型:選擇題
| x | -2 | -1 | 0 | 1 | 2 |
| y | 5 | 2 | 2 | 1 |
| A. | 3 | B. | 4 | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | (0,1) | D. | $({0,\frac{1}{2}})∪$$({\frac{1}{2},1})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 12種 | B. | 13種 | C. | 14種 | D. | 15種 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
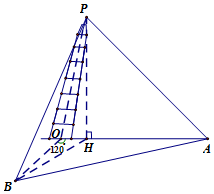 上海市松江區天馬山上的“護珠塔”因其傾斜度超過意大利的比薩斜塔而號稱“世界第一斜塔”.興趣小組同學實施如下方案來測量塔的傾斜度和塔高:如圖,記O點為塔基、P點為塔尖、點P在地面上的射影為點H.在塔身OP射影所在直線上選點A,使仰角k∠HAP=45°,過O點與OA成120°的地面上選B點,使仰角∠HPB=45°(點A、B、O都在同一水平面上),此時測得∠OAB=27°,A與B之間距離為33.6米.試求:
上海市松江區天馬山上的“護珠塔”因其傾斜度超過意大利的比薩斜塔而號稱“世界第一斜塔”.興趣小組同學實施如下方案來測量塔的傾斜度和塔高:如圖,記O點為塔基、P點為塔尖、點P在地面上的射影為點H.在塔身OP射影所在直線上選點A,使仰角k∠HAP=45°,過O點與OA成120°的地面上選B點,使仰角∠HPB=45°(點A、B、O都在同一水平面上),此時測得∠OAB=27°,A與B之間距離為33.6米.試求:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com