
分析 (1)由題意可知:當a=8時,f(x)=$\frac{8}{x}$+lnx-2,(x>0),求導,f′(x)=-$\frac{8}{{x}^{2}}$+$\frac{1}{x}$=$\frac{x-8}{{x}^{2}}$(x>0),令f′(x)>0,求得函數的單調遞增區間,令f′(x)<0,求得函數的單調遞減區間;
(2)求導f′(x)=-$\frac{a}{{x}^{2}}$+$\frac{1}{x}$=$\frac{x-a}{{x}^{2}}$,(x>0),當a≤0,f′(x)>0恒成立,即f(x)在(0,e2]上單調遞增,無最小值;當a>0,令f′(x)=0,得x=a,根據函數的單調性可知:若a>e2,則函數f(x)在(0,e2]上的最小值f(x)min=f(e2)=$\frac{a}{{e}^{2}}$+lne2-2=$\frac{a}{{e}^{2}}$,a=2e2,滿足a>e2,符合題意;若0<a≤e2,則函數f(x)在(0,e2]上的最小值f(x)min=f(a)=$\frac{a}{a}$+lna-2=lna-1,解得:a=e3,不滿足0<a≤e2,不符合題意,舍去.
解答 解:(1)當a=8時,f(x)=$\frac{8}{x}$+lnx-2,(x>0),
∴f′(x)=-$\frac{8}{{x}^{2}}$+$\frac{1}{x}$=$\frac{x-8}{{x}^{2}}$(x>0),
令f′(x)>0,即$\frac{x-8}{{x}^{2}}$>0,解得:x>8,
令f′(x)<0,即$\frac{x-8}{{x}^{2}}$<0,解得:0<x<8,
∴f(x)的單調遞減區間為(0,8),單調遞增區間為(8,+∞);…(4分)
(2)由f(x)=$\frac{a}{x}$+lnx-2,求導f′(x)=-$\frac{a}{{x}^{2}}$+$\frac{1}{x}$=$\frac{x-a}{{x}^{2}}$,(x>0),
(i)當a≤0,f′(x)>0恒成立,即f(x)在(0,e2]上單調遞增,無最小值,不滿足題意.
(ii)當a>0,令f′(x)=0,得x=a,
∴當f′(x)>0時,x>a,當f′(x)<0時,x<a,
∴f(x)在(0,a)上單調遞減,在(a,+∞)上單調遞增.
若a>e2,則函數f(x)在(0,e2]上的最小值f(x)min=f(e2)=$\frac{a}{{e}^{2}}$+lne2-2=$\frac{a}{{e}^{2}}$,
由$\frac{a}{{e}^{2}}$=2,解得:a=2e2,滿足a>e2,符合題意;
若0<a≤e2,則函數f(x)在(0,e2]上的最小值f(x)min=f(a)=$\frac{a}{a}$+lna-2=lna-1,
由lna-1=2,解得:a=e3,不滿足0<a≤e2,不符合題意,舍去.
綜上可知,存在實數a=2e2,使函數f(x)在(0,e2]上有最小值2.…(12分)
點評 本題考查導數的綜合應用,考查利用導數求函數的單調性及最值,考查導數的運算,考查分類討論思想,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,2) | B. | [$\frac{13}{4}$,2) | C. | [$\frac{13}{8}$,2) | D. | (-∞,$\frac{13}{8}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({-1,\frac{1}{2}})$ | B. | $({-∞,\frac{1}{2}})$ | C. | $({\frac{1}{2},2})$ | D. | $[{-1,\frac{1}{2}})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
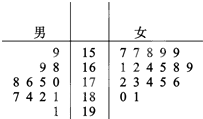 某部隊為了在大閱兵中樹立軍隊的良好形象,決定從參訓的12名男兵和18名女兵中挑選出正式閱兵人員,這30名軍人的身高如圖:單位:cm
某部隊為了在大閱兵中樹立軍隊的良好形象,決定從參訓的12名男兵和18名女兵中挑選出正式閱兵人員,這30名軍人的身高如圖:單位:cm查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $C_7^5×{({\frac{1}{3}})^2}×{({\frac{2}{3}})^5}$ | B. | $C_7^5×{({\frac{1}{3}})^2}×{({\frac{1}{3}})^5}$ | C. | $C_7^3×{({\frac{1}{3}})^2}×{({\frac{2}{3}})^5}$ | D. | $C_7^2×{({\frac{2}{3}})^2}×{({\frac{1}{3}})^5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com