
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①m∥n或m,n相交或m,n異面;②由面面垂直的判定定理可得α⊥β;③n∥α或n?α,④n⊥α或n⊥β,但也有可能n與α,β斜交.
解答 解:①若m∥α,n∥β,α∥β,則m∥n或m,n相交或m,n異面,故①錯誤
②若m∥n,m?α,則
當n?α時,根據線面平行的判定定理可得n∥α,由n⊥β可得α⊥β,
當n?α時,由n⊥β,則可得m⊥β,由平面垂直的判定定理可得,α⊥β,故②正確
③若α∩β=m,m∥n,
當n⊆α時,滿足已知;當n?α時,由線面平行的判定定理可得則n∥α
n與β的關系同理可判斷,故③錯誤
④若m⊥n,α∩β=m,
若n⊆β,由線面垂直的判定定理可得則n⊥α或
若n⊆α,由線面垂直的判定定理可得n⊥β.
n?α,n?β時,n與α,β不垂直,即有可能n與α,β斜交,故④錯誤
故選A.
點評 本題主要題考查的知識點是平面的基本性質及推論,空間直線與平面位置關系的判斷,其中根據面面平行,線面垂直的判定及性質,空間直線與平面位置關系的定義和幾何特征.


科目:高中數學 來源: 題型:解答題
 在四棱錐P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G為PC的中點,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分別為BC,EG上一點,且AF∥CD.
在四棱錐P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G為PC的中點,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分別為BC,EG上一點,且AF∥CD.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
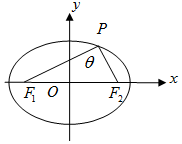 橢圓$\frac{x^2}{4}+{y^2}$=1上的一點P與兩焦點F1,F2所構成的三角形稱為焦點三角形.
橢圓$\frac{x^2}{4}+{y^2}$=1上的一點P與兩焦點F1,F2所構成的三角形稱為焦點三角形.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
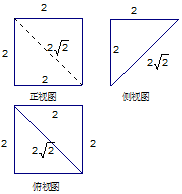
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $3-2\sqrt{2}$ | B. | $2-\sqrt{2}$ | C. | $\sqrt{3}-\sqrt{2}$ | D. | $\sqrt{2}-1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com