
| 用水量t(單位:噸) | 每噸收費標準(單位:元) |
| 不超過2噸部分 | m |
| 超過2噸不超過4噸部分 | 3 |
| 超過4噸部分 | n |
分析 (1)由題意,當t=3.5時,y=7.5;當t=6時,y=21,從而求出m,n;再由分段函數寫出表達式;
(2)分析分段函數在各段上的取值范圍,從而得到6t-15≤18,從而求用水量.
解答 解:(1)由已知y=$\left\{\begin{array}{l}{mt,0≤t≤2}\\{3t-3,2<t≤4}\\{nt-15,t>4}\end{array}\right.$
當t=3.5時,y=7.5;當t=6時,y=21.
代入得:$\left\{{\begin{array}{l}{2m+4.5=7.5}\\{2m+6+2n=21}\end{array}}\right.$解得:m=1.5,n=6
∴y關于t的函數關系式為:$y=\left\{{\begin{array}{l}{1.5t,0≤t≤2}\\{3t-3,2<t≤4}\\{6t-15.t>4}\end{array}}\right.$
(2)令6t-15≤18,解得t≤5.5
∴該用戶最多用水量為5.5噸.
點評 本題考查了分段函數的應用,同時考查了將實際問題轉化為數學問題的能力,屬于中檔題,


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (2,+∞) | B. | (2,4] | C. | (-∞,4] | D. | (2,4) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=x,$g(x)=\frac{x^2}{x}$ | B. | $f(x)=\sqrt{x^2}$,$g(x)=\left\{\begin{array}{l}x,x≥0\\-x,x<0\end{array}\right.$ | ||
| C. | $f(x)={(\sqrt{x})^2}$,g(x)=x | D. | $f(x)=\sqrt{x^2}$,$g(x)=\root{3}{x^3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
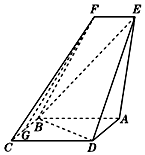 如圖,四邊形ABCD是平行四邊形,AE⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G為BC的中點.
如圖,四邊形ABCD是平行四邊形,AE⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G為BC的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com