
| A. | $\frac{{e-\sqrt{{e^2}-1}}}{e}$ | B. | $\frac{{2\sqrt{{e^2}+1}-e}}{2e}$ | C. | $\frac{{\sqrt{{e^2}+1}-e}}{2e}$ | D. | $e+\frac{1}{e}-\frac{1}{2}$ |
分析 由圓的對稱性可得只需考慮圓心C(e+$\frac{1}{e}$,0)到函數f(x)=lnx圖象上一點的距離的最小值.設f(x)圖象上一點P(m,lnm),求得切線的斜率,由兩直線垂直的條件:斜率之積為-1,可得lnm+m2-(e+$\frac{1}{e}$)m=0,由g(x)=lnx+x2-(e+$\frac{1}{e}$)x,求出導數,判斷單調性,可得零點e,運用兩點的距離公式計算即可得到所求值
解答 解:由圓的對稱性可得只需考慮圓心C(e+$\frac{1}{e}$,0)到函數f(x)=lnx圖象上一點的距離的最小值.
設f(x)圖象上一點(m,lnm),
由f(x)的導數為f′(x)=$\frac{1}{x}$,即有切線的斜率為k=$\frac{1}{m}$,
可得$\frac{lnm-0}{m-(e+\frac{1}{e})}$=-m,
即有lnm+m2-(e+$\frac{1}{e}$)m=0,
由g(x)=lnx+x2-(e+$\frac{1}{e}$)x,可得g′(x)=$\frac{1}{x}$+2x-(e+$\frac{1}{e}$),
當2<x<3時,g′(x)>0,g(x)遞增.
又g(e)=lne+e2-(e+$\frac{1}{e}$)•e=0,
可得x=e處點P(e,1)到點Q的距離最小,且為$\sqrt{1+\frac{1}{{e}^{2}}}$,
則線段PQ的長度的最小值為$\sqrt{1+\frac{1}{{e}^{2}}}$-$\frac{1}{2}$=$\frac{2\sqrt{{e}^{2}+1}-e}{2e}$.
故選:B.
點評 本題考查導數的運用:求切線的斜率和單調性,考查圓的對稱性和兩點的距離公式,考查運算能力,屬于中檔題.


 53天天練系列答案
53天天練系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5π}{2}$ | B. | $\frac{5π}{4}$ | C. | $\frac{3+π}{2}$ | D. | 3+π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 做米飯需要刷鍋,淘米,添水,加熱這些步驟 | |
| B. | 洗衣機的使用說明書 | |
| C. | 利用公式S=πr2計算半徑為4的圓的面積,就是計算π×42 | |
| D. | 解方程2x2+x-1=0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
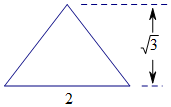 一個四棱錐的側棱長都相等,底面是正方形,且其正視圖為如圖所示的等腰三角形,則該四棱錐的體積是( )
一個四棱錐的側棱長都相等,底面是正方形,且其正視圖為如圖所示的等腰三角形,則該四棱錐的體積是( )| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $2\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $y=x+\frac{4}{x}$ | B. | $y=sinx+\frac{4}{sinx}(0<x<π)$ | ||
| C. | y=4log3x+logx3 | D. | y=4ex+e-x |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com