
分析 (1)求出函數的導數,利用導函數大于0,分半求解a,b的值即可.
(2)畫出函數的圖象,求出曲線的斜率,然后推出結果.
解答 解:(Ⅰ)f′(x)=2x+a,∴f′(0)f′(1)=-1,即a(a+2)=-1,a=-1.
g(x)=x2-x+$\frac{b}{2}$lnx-bx,g′(x)=2x-1+$\frac{b}{2x}$-b≥0在x>0上恒成立,即(2x-1)(1-$\frac{b}{2x}$)≥0,
當x≥$\frac{1}{2}$時,b≤2x,即b≤1;當0<x≤$\frac{1}{2}$時,b≥2x,即b≥1,故b=1.(6分)
(Ⅱ)由題意y=h(x)與y=kx有四個交點.如圖,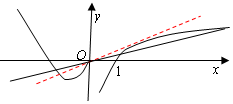
設直線y=kx與曲線y=lnx切于(x0,lnx0),則k=$\frac{1}{x_0}$,
∴lnx0=$\frac{1}{x_0}$×x0=1,$\frac{1}{x_0}$=$\frac{1}{e}$,由圖可知k∈(0,$\frac{1}{e}$).(12分)
點評 本題考查函數的導數的綜合應用,函數的單調性以及函數的零點個數的判斷,是中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | ?x>0,cosx+sinx>1 | B. | ?x0≤0,cosx0+sinx0≤1 | ||
| C. | ?x>0,cosx+sinx≤1 | D. | ?x0>0,cosx0+sinx0≤1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2P |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a>0 | B. | $0<a<\sqrt{2}$ | C. | 0<a<2 | D. | 以上都不對 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-1,+∞) | B. | [-1,5)∪(5,+∞) | C. | [-1,5) | D. | (5,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
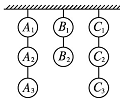 在一次射擊比賽中,8個泥制的靶子掛成三列,其中兩列各掛3個,一列掛2個,一射手射擊時只準擊碎三列靶子任一列中最下面的一個,若每次射擊都遵循這條原則,則擊碎8個靶子可以有多少種不同的次序?
在一次射擊比賽中,8個泥制的靶子掛成三列,其中兩列各掛3個,一列掛2個,一射手射擊時只準擊碎三列靶子任一列中最下面的一個,若每次射擊都遵循這條原則,則擊碎8個靶子可以有多少種不同的次序?查看答案和解析>>
科目:高中數學 來源: 題型:解答題
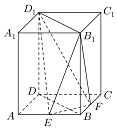 如圖,在正四棱柱ABCD-A1B1C1D1中,底面邊長為2$\sqrt{2}$,側棱長為4,E、F分別
如圖,在正四棱柱ABCD-A1B1C1D1中,底面邊長為2$\sqrt{2}$,側棱長為4,E、F分別查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-3,1]∪[3,+∞) | B. | [-3,1]∪[2,+∞) | C. | [-1,1]∪[3,+∞) | D. | (-∞,-3]∪[1,3] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com