
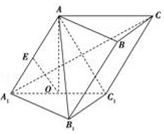
 如圖,在斜三棱柱ABC-A1B1C1中,點O、E分別是A1C1、AA1的中點,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.
如圖,在斜三棱柱ABC-A1B1C1中,點O、E分別是A1C1、AA1的中點,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.分析 (1)由中位線定理得出OE∥AC1,故而OE∥平面AB1C1;
(2)通過證明A1C⊥平面AB1C1得出AB1⊥A1C;
(3)利用等體積得出C1到平面AA1B1的距離d,即可得出P到側面ABB1A的距離.
解答 證明:(1)∵點O、E分別是A1C1、AA1的中點,
∴OE∥AC1,
又∵EO?平面AB1C1,AC1?平面AB1C1,
∴OE∥平面AB1C1,
(2)∵AO⊥平面A1B1C1,B1C1?平面A1B1C1,
∴AO⊥B1C1,
又∵A1C1⊥B1C1,A1C1∩AO=O,
∴B1C1⊥平面A1C1CA,又A1C?平面A1C1CA,
∴A1C⊥B1C1.
∵AA1=AC,∴四邊形A1C1CA為棱形,
∴A1C⊥AC1,又B1C1∩AC1=C1,B1C1?平面AB1C1,AC1?平面AB1C1,
∴A1C⊥平面AB1C1,又AB1?平面AB1C1,
∴AB1⊥A1C.
(3)解:由題意,P到側面ABB1A的距離等于點C1到平面AA1B1的距離.
∵∠BCA=90°,AA1=AC=BC=2,
∴A1O=$\frac{1}{2}$A1C1=1,AC1=2,
∴AO=$\sqrt{3}$,A1B1=2$\sqrt{2}$,AB1=2$\sqrt{2}$,
∴${S}_{△{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{2}×2×2$=2,${S}_{△A{A}_{1}{B}_{1}}$=$\frac{1}{2}×2×\sqrt{8-1}$=$\sqrt{7}$
∴${V}_{A-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{3}$×2×$\sqrt{3}$=$\frac{2\sqrt{3}}{3}$.
設點C1到平面AA1B1的距離為d,則$\frac{2\sqrt{3}}{3}$=$\frac{1}{3}$×$\sqrt{7}$×d,即d=$\frac{2\sqrt{21}}{7}$,
∴P到側面ABB1A的距離等于$\frac{2\sqrt{21}}{7}$.
點評 本題考查了線面平行的判定,線面垂直的判定,空間距離的計算,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 1200 | B. | 600 | C. | 450 | D. | 300 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com