
分析 (Ⅰ)由題意的A、B兩點(diǎn)關(guān)于y軸對(duì)稱,圓心E到AB的距離為1,求出B坐標(biāo)代入橢圓方程得a即可.
(Ⅱ)設(shè)M(x1,y1),N(x2,y2),N′(-x2,y2).圓E交y軸負(fù)半軸于點(diǎn)D(0,-$\frac{1}{2}$),當(dāng)直線MN斜率存在時(shí),設(shè)其方程為:y=kx-$\frac{1}{2}$,直線MN′的方程$y-{y}_{1}=\frac{{y}_{1}-{y}_{2}}{{x}_{1}+{x}_{2}}(x-{x}_{1})$,依據(jù)橢圓的對(duì)稱性,若直線MN'過定點(diǎn),定點(diǎn)一定在y軸上,令x=0,$y={y}_{1}-\frac{{x}_{1}({y}_{1}-{y}_{2})}{{x}_{1}+{x}_{2}}=\frac{{x}_{1}{y}_{2}+{y}_{2}{x}_{1}}{{x}_{1}+{x}_{2}}$=$\frac{{x}_{1}(k{x}_{2}-\frac{1}{2})+{x}_{2}(k{x}_{1}+\frac{1}{2})}{{x}_{1}+{x}_{2}}$=$\frac{2k{x}_{1}{x}_{2}}{{x}_{1}+{x}_{2}}-\frac{1}{2}=-2$.
解答 解:(Ⅰ)由題意的A、B兩點(diǎn)關(guān)于y軸對(duì)稱,∵${x}_{B}=\sqrt{3}$,
圓心E到AB的距離為1,∴${y}_{B}=\frac{1}{2}$,∴$B(\sqrt{3},\frac{1}{2})$,代入橢圓方程得$\frac{3}{{a}^{2}}+\frac{1}{4}=1$,
解得a2=4,∴$e=\frac{\sqrt{3}}{2}$.
(Ⅱ)設(shè)M(x1,y1),N(x2,y2),N′(-x2,y2).
圓E交y軸負(fù)半軸于點(diǎn)D(0,-$\frac{1}{2}$),
當(dāng)直線MN斜率存在時(shí),設(shè)其方程為:y=kx-$\frac{1}{2}$,
$\left\{\begin{array}{l}{y=kx-\frac{1}{2}}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$消去y得(1+4k2)x2-4kx-3=0.
∴x1+x2=$\frac{4k}{1+4{k}^{2}}$,x1x2=$\frac{-3}{1+4{k}^{2}}$,
直線MN′的方程$y-{y}_{1}=\frac{{y}_{1}-{y}_{2}}{{x}_{1}+{x}_{2}}(x-{x}_{1})$,
依據(jù)橢圓的對(duì)稱性,若直線MN'過定點(diǎn),定點(diǎn)一定在y軸上,
令x=0,$y={y}_{1}-\frac{{x}_{1}({y}_{1}-{y}_{2})}{{x}_{1}+{x}_{2}}=\frac{{x}_{1}{y}_{2}+{y}_{2}{x}_{1}}{{x}_{1}+{x}_{2}}$=$\frac{{x}_{1}(k{x}_{2}-\frac{1}{2})+{x}_{2}(k{x}_{1}+\frac{1}{2})}{{x}_{1}+{x}_{2}}$=$\frac{2k{x}_{1}{x}_{2}}{{x}_{1}+{x}_{2}}-\frac{1}{2}=-2$.
當(dāng)直線MN斜率不存在時(shí),直線MN′的方程為x=0,顯然過點(diǎn)(0,-2).
直線MN'過定點(diǎn)(0,-2)
點(diǎn)評(píng) 本題考查了橢圓與圓的綜合應(yīng)用,及直線過定點(diǎn)問題,屬于難題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | π | B. | 3π | C. | 8π | D. | 9π |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
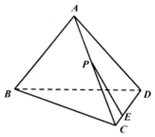 如圖,已知三棱錐A-BCD的所有棱長(zhǎng)均相等,點(diǎn)E滿足$\overrightarrow{DE}$=3$\overrightarrow{EC}$,點(diǎn)P在棱AC上運(yùn)動(dòng),設(shè)EP與平面BCD所成角為θ,則sinθ的最大值為$\frac{2\sqrt{2}}{3}$.
如圖,已知三棱錐A-BCD的所有棱長(zhǎng)均相等,點(diǎn)E滿足$\overrightarrow{DE}$=3$\overrightarrow{EC}$,點(diǎn)P在棱AC上運(yùn)動(dòng),設(shè)EP與平面BCD所成角為θ,則sinθ的最大值為$\frac{2\sqrt{2}}{3}$.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com