
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\sqrt{3}$ |
分析 分別聯立直線方程和雙曲線方程,直線方程和拋物線方程,消去y,運用中點坐標公式,可得AB,CD的中點坐標公式,再由雙曲線的基本量a,b,c的關系和離心率公式,即可得到所求值.
解答 解:聯立直線l:y=x-1,雙曲線c1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,
可得(b2-a2)x2+2a2x+a2-a2b2=0,
直線l與c1相交于A,B兩點,
可得AB的中點坐標為(-$\frac{{a}^{2}}{{b}^{2}-{a}^{2}}$,$\frac{{b}^{2}}{{a}^{2}-{b}^{2}}$),
聯立直線l:y=x-1,拋物線c2:y2=2x,
可得x2-4x+1=0,
直線l與c2相交于C,D兩點,
則CD的中點為(2,1),
若線段AB與CD的中點相同,
可得$\frac{{b}^{2}}{{a}^{2}-{b}^{2}}$=1,即a2=2b2,
即為a2=2(c2-a2)
即有2c2=3a2,
則e=$\frac{c}{a}$=$\frac{\sqrt{6}}{2}$.
故選:A.
點評 本題考查直線方程和雙曲線方程,拋物線方程聯立,注意運用中點坐標公式,考查雙曲線的離心率的求法,屬于中檔題.


 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
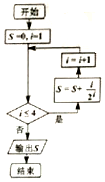
| A. | $\frac{15}{16}$ | B. | $\frac{15}{12}$ | C. | $\frac{13}{8}$ | D. | $\frac{13}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題

查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 如果a1是5的倍數,那么數列{an}與數列{2n}必有相同的項 | |
| B. | 如果a1不是5的倍數,那么數列{an}與數列{2n}必沒有相同的項 | |
| C. | 如果a1不是5的倍數,那么數列{an}與數列{2n}只有有限個相同的項 | |
| D. | 如果a1不是5的倍數,那么數列{an}與數列{2n}有無窮多個相同的項. |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-3,3] | B. | $[-\frac{3}{2},3]$ | C. | $[-3,\frac{{3\sqrt{3}}}{2}]$ | D. | $[-3,\frac{3}{2}]$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com