
分析 (1)利用誘導公式,降冪公式化簡函數解析式可得f(x)=cos2x+$\frac{1}{2}$,利用周期公式可求最小正周期,根據余弦函數的單調性可求單調遞減區間.
(2)由(1)及f($\frac{A}{2}$)=1可求A,利用余弦定理,基本不等式可求bc≤4,進而利用三角形面積公式即可得解面積的最大值.
解答 解:(1)∵$f(x)=\frac{1}{2}sin(2x+\frac{π}{2})+\frac{1+cos2x}{2}$=$\frac{1}{2}cos2x+\frac{1}{2}cos2x+\frac{1}{2}=cos2x+\frac{1}{2}$.
∴T=$\frac{2π}{2}$=π.
∵令$2kπ≤2x≤2kπ+π⇒kπ≤x≤kπ+\frac{π}{2}$,k∈Z,
∴f(x)的單調遞減區間為$[kπ,kπ+\frac{π}{2}]$,k∈Z.
(2)∵$f(\frac{A}{2})=1⇒cosA+\frac{1}{2}=1⇒cosA=\frac{1}{2}⇒A=\frac{π}{3}$.
又∵a=2,
∴a2=b2+c2-2bccosA,可得:4=b2+c2-bc≥bc,
∴bc≤4.
∴${S_{△ABC}}=\frac{1}{2}bcsinA$$≤\frac{1}{2}×4×\frac{{\sqrt{3}}}{2}=\sqrt{3}$,當且僅當b=c=2時取等號.
點評 本題主要考查了誘導公式,降冪公式,周期公式,余弦函數的單調性,余弦定理,基本不等式,三角形面積公式在解三角形中的綜合應用,考查了轉化思想,屬于基礎題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -a>-b | B. | a+c>b+c | C. | $\frac{1}{a}>\frac{1}{b}$ | D. | (-a)2>(-b)2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | -$\frac{5}{3}$ | C. | -$\frac{1}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
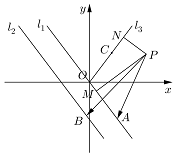 如圖,已知直線l1:kx+y=0和直線l2:kx+y+b=0(b>0),射線OC的一個法向量為$\overrightarrow{n_3}$=(-k,1),點O為坐標原點,且k≥0,直線l1和l2之間的距離為2,點A、B分別是直線l1、l2上的動點,P(4,2),PM⊥l1于點M,PN⊥OC于點N;
如圖,已知直線l1:kx+y=0和直線l2:kx+y+b=0(b>0),射線OC的一個法向量為$\overrightarrow{n_3}$=(-k,1),點O為坐標原點,且k≥0,直線l1和l2之間的距離為2,點A、B分別是直線l1、l2上的動點,P(4,2),PM⊥l1于點M,PN⊥OC于點N;查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 命題“?x0∈R,${x_0}^2-{x_0}≤0$”的否定為“?x∈R,x2-x>0” | |
| B. | 命題“在△ABC中,A>30°,則$sinA>\frac{1}{2}$”的逆否命題為真命題 | |
| C. | 若非零向量$\overrightarrow a$、$\overrightarrow b$滿足$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$,則$\overrightarrow a$與$\overrightarrow b$共線 | |
| D. | 設{an}是公比為q的等比數列,則“q>1”是“{an}為遞增數列”的充分必要條件 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com