
分析 根據向量的數量積公式和向量的夾角公式計算即可.
解答 解:∵|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,$\overrightarrow{a}$與$\overrightarrow{b}$的夾角為60°,
∴$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos60°=2×1×$\frac{1}{2}$=1,
∴($\overrightarrow{a}$+2$\overrightarrow{b}$)($\overrightarrow{a}$-$\overrightarrow{b}$)=|$\overrightarrow{a}$|2-2|$\overrightarrow{b}$|2+$\overrightarrow{a}•\overrightarrow{b}$=4-2+1=3,
∴($\overrightarrow{a}$+2$\overrightarrow{b}$)2=|$\overrightarrow{a}$|2+4|$\overrightarrow{b}$|2+4$\overrightarrow{a}•\overrightarrow{b}$=4+4+4=12,($\overrightarrow{a}$-$\overrightarrow{b}$)2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2-2$\overrightarrow{a}•\overrightarrow{b}$=4+1-2=3,
∴|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2$\sqrt{3}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{3}$,
設向量$\overrightarrow{a}$+2$\overrightarrow{b}$與$\overrightarrow{a}$-$\overrightarrow{b}$的夾角為θ,
∴cosθ=$\frac{(\overrightarrow{a}+2\overrightarrow{b})•(\overrightarrow{a}-\overrightarrow{b})}{|\overrightarrow{a}+2\overrightarrow{b}|•|\overrightarrow{a}-\overrightarrow{b}|}$=$\frac{3}{2\sqrt{3}×\sqrt{3}}$=$\frac{1}{2}$.
點評 本題考查了向量的數量積公式和向量的夾角公式,屬于基礎題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 以上都不對 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
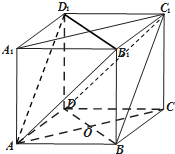 在正方體ABCD-A1B1C1D1中,O是底面ABCD對角線的交點.
在正方體ABCD-A1B1C1D1中,O是底面ABCD對角線的交點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (2-$\sqrt{2}$,1] | B. | (2-$\sqrt{2}$,2+$\sqrt{2}$] | C. | (-∞,2-$\sqrt{2}$)∪(2+$\sqrt{2}$,+∞) | D. | [-1,$\sqrt{2}$-2) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com