Question

8．已知函數F（x）=sinx•f′（x）是定義在R上的偶函數，且當x≥0時，f（x）=2a|x-1|-a，其中a＞0為常數．若函數y=f[f（x）]有10個零點，則a的取值范圍是$（\frac{1}{2}，\frac{3}{2}）$．

Answer 1

分析 利用函數是偶函數，通過x＞0求出f（x）的零點，畫出函數的圖象，判斷x＞0時由5個零點，推出結果即可．

解答 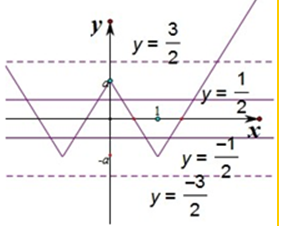解：當x≥0時，f（x）=2a|x-1|-a=a（2|x-1|-1）=0，可得2|x-1|-1=0，解得x=$\frac{1}{2}$或x=$\frac{3}{2}$，
∵f（x）是偶函數，∴當x＜0時，f（x）=0的另外兩個解為：$-\frac{1}{2}$和$-\frac{3}{2}$，由選項可得a＞0，
作出函數的圖象如圖：
設t=f（x），則有y=f（f（x））=0得，f（t）=0，
可得t=$±\frac{1}{2}$或$±\frac{3}{2}$，
∵f（x）是偶函數，
∴要使函數y=f（f（x））恰有10個零點，
則等價于x＞0時，y=f（f（x））恰有5個零點，有函數的圖象可得：$\left\{\begin{array}{l}{\frac{1}{2}＜a}\\{\frac{3}{2}＞a}\end{array}\right.$，即$\frac{1}{2}＜a＜\frac{3}{2}$．
故答案為：$（\frac{1}{2}，\frac{3}{2}）$．

點評 本題考查函數的單調性，考查函數的零點，考查函數的周期性與奇偶性，利用數形結合的思想來求解，會化難為易．