
分析 (1)當n=1時,S1=2a1-4,a1=4,當n≥2時,${a_n}={S_n}-{S_{n-1}}=2{a_n}-{2^{n+1}}-2{a_{n-1}}+{2^n}$,整理得:$\frac{a_n}{2^n}-\frac{{{a_{n-1}}}}{{{2^{n-1}}}}=1$,可得bn-bn-1=1,${b_1}=\frac{a_1}{2}=2$,{bn}是首項為2,公差為1的等差數列;
(2)由(1)可知:${c_n}={b_n}•{2^{-n}}=(n+1)•\frac{1}{2^n}$,利用“錯位相減法”即可求得${T_n}=3-\frac{2}{2^n}-\frac{n+1}{2^n}=3-\frac{n+3}{2^n}<3$;
(3)由dn+1>dn得4n+1+(-1)nλ•2n+2>4n+(-1)n-1λ•2n+1,整理得:2n-1+(-1)nλ>0,當n為奇數時,λ<2n-1,λ<1;當n為偶數時,λ>-2n-1,λ>-2,由λ為非零整數,即可求得λ=-1.
解答 解:(1)證明:當n=1時,S1=2a1-4,
∴a1=4,
當n≥2時,${a_n}={S_n}-{S_{n-1}}=2{a_n}-{2^{n+1}}-2{a_{n-1}}+{2^n}$,
∴${a_n}-2{a_{n-1}}={2^n}$,即$\frac{a_n}{2^n}-\frac{{{a_{n-1}}}}{{{2^{n-1}}}}=1$,
∴bn-bn-1=1(常數),
又${b_1}=\frac{a_1}{2}=2$,
∴{bn}是首項為2,公差為1的等差數列,bn=n+1.
(2)證明:由(1)可知:${c_n}={b_n}•{2^{-n}}=(n+1)•\frac{1}{2^n}$,
${T_n}=\frac{2}{2}+\frac{3}{2^2}+…+\frac{n+1}{2^n}$,
相減得$\frac{1}{2}{T_n}=1+\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{2^n}-\frac{n+1}{{{2^{n+1}}}}$,
=$1+\frac{{\frac{1}{2^2}(1-\frac{1}{{{2^{n-1}}}})}}{{1-\frac{1}{2}}}-\frac{n+1}{{{2^{n+1}}}}$,
=$\frac{3}{2}-\frac{1}{2^n}-\frac{n+1}{{{2^{n+1}}}}$,
∴${T_n}=3-\frac{2}{2^n}-\frac{n+1}{2^n}=3-\frac{n+3}{2^n}<3$.
(3)由dn+1>dn得4n+1+(-1)nλ•2n+2>4n+(-1)n-1λ•2n+1,
3•4n+(-1)nλ•2n+2+(-1)nλ•2n+1>0,
3•4n+(-1)nλ•2n+1×3>0,
2n-1+(-1)nλ>0,
當n為奇數時,λ<2n-1,
∴λ<1;
當n為偶數時,λ>-2n-1,
∴λ>-2,
∴-2<λ<1,
又λ為非零整數,
∴λ=-1.
點評 本題考查等差數列的性質及通項公式,“錯位相減法”求數列的前n項和,不等式的性質,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
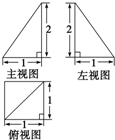
| A. | 2+$\sqrt{5}$ | B. | 3+$\frac{\sqrt{5}}{2}$ | C. | 2+$\frac{\sqrt{5}}{2}$ | D. | 3+$\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-2,2) | B. | (-∞,-2)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,0)∪(2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
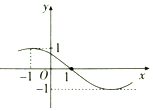
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 函數f(x)無極值點 | B. | x=1為f(x)的極小值點 | ||
| C. | x=2為f(x)的極大值點 | D. | x=2為f(x)的極小值點 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com