Question

20．函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，0≤φ＜2π）的部分圖象如圖所示，則f（x）=sin（$\frac{π}{4}$x+$\frac{3π}{4}$）

Answer 1

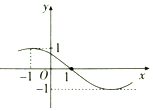
分析 由題意易得A值和周期，可得ω，代入點（-1，1）的坐標計算可得φ值，可得解析式．

解答 解：由題意可得A=1，周期T=$\frac{2π}{ω}$=4[1-（-1）]=8，
解得：ω=$\frac{π}{4}$，
∴f（x）=sin（$\frac{π}{4}$x+φ），
由函數圖象過點（-1，1），可得1=sin（-$\frac{π}{4}$+φ），
∴-$\frac{π}{4}$+φ=kπ+$\frac{π}{2}$，k∈Z，由0≤φ＜2π，可得φ=$\frac{3π}{4}$，
故函數的解析式為f（x）=sin（$\frac{π}{4}$x+$\frac{3π}{4}$）．
故答案為：sin（$\frac{π}{4}$x+$\frac{3π}{4}$）．

點評 本題主要考查了由y=Asin（ωx+φ）的部分圖象確定其解析式，考查了數形結合思想，屬于基礎題．