
分析 (Ⅰ)根據已知設橢圓的焦距2c,當y=c時,|MN|=|x1-x2|=$\frac{2{b}^{2}}{a}$,由題意得,△MNF2的面積為$\frac{1}{2}×$|MN|×|F1F2|=c|MN|=$\frac{2{b}^{2}c}{a}=\sqrt{3}$,又∵$\frac{c}{a}=\frac{\sqrt{3}}{2}$,解得a、b即可.
(Ⅱ)設A(x1,y1),B(x2,y2),P(0,y0),分類討論:當m=0時,利用橢圓的對稱性即可得出;m≠0時,直線AB的方程與橢圓的方程聯立得到△>0及根與系數的關系,再利用向量相等,代入計算即可得出.
解答 解:(Ⅰ)根據已知設橢圓的焦距2c,當y=c時,|MN|=|x1-x2|=$\frac{2{b}^{2}}{a}$,
由題意得,△MNF2的面積為$\frac{1}{2}×$|MN|×|F1F2|=c|MN|=$\frac{2{b}^{2}c}{a}=\sqrt{3}$,
又∵$\frac{c}{a}=\frac{\sqrt{3}}{2}$,解得b2=1,a2=4,
橢圓C的標準方程為:x2+$\frac{{y}^{2}}{4}=1$.
(Ⅱ)當m=0時,則P(0,0),由橢圓的對稱性得$\overrightarrow{AP}=\overrightarrow{PB},即\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{0}$,
∴m=0時,存在實數λ,使得$\overrightarrow{OA}$+λ$\overrightarrow{OB}$=4$\overrightarrow{OP}$,
當m≠0時,由$\overrightarrow{OA}$+λ$\overrightarrow{OB}$=4$\overrightarrow{OP}$,得$\overrightarrow{OP}=\frac{1}{4}\overrightarrow{OA}+\frac{λ}{4}\overrightarrow{OB}$,
∵A、B、p三點共線,∴1+λ=4,⇒λ=3⇒$\overrightarrow{AP}=3\overrightarrow{PB}$
設A(x1,y1),B(x2,y2)
由$\left\{\begin{array}{l}{y=kx+m}\\{4{x}^{2}+{y}^{2}-4=0}\end{array}\right.$,得(k2+4)x2+2mkx+m2-4=0,
由已知得△=4m2k2-4(k2+4)(m2-4)>0,即k2-m2+4>0
且x1+x2=$\frac{-2km}{{k}^{2}+4}$,x1x2=$\frac{{m}^{2}-4}{{k}^{2}+4}$.
由$\overrightarrow{AP}=3\overrightarrow{PB}$得x1=-3x2
3(x1+x2)2+4x1x2=0,∴$\frac{12{k}^{2}{m}^{2}}{({k}^{2}+4)^{2}}+\frac{4({m}^{2}-4)}{{k}^{2}+4}=0$,⇒m2k2+m2-k2-4=0
顯然m2=1不成立,∴${k}^{2}=\frac{4-{m}^{2}}{{m}^{2}-1}$
∵k2-m2+4>0,∴$\frac{4-{m}^{2}}{{m}^{2}-1}-{m}^{2}+4>0$,即$\frac{(4-{m}^{2}){m}^{2}}{{m}^{2}-1}>0$.
解得-2<m<-1或1<m<2.
綜上所述,m的取值范圍為(-2,-1)∪(1,2)∪{0}
點評 本題考查橢圓的標準方程的求法,考查了橢圓的簡單性質、涉及直線與橢圓相交問題,常轉化為關于x的一元二次方程,利用△>0及根與系數的關系、向量相等等基礎知識與基本技能方法求解,考查了推理能力和計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
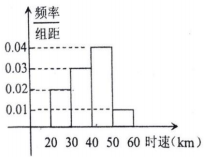 太原市某時段100輛汽車通過祥云橋時,時速的頻率分布直方圖如圖所示,則時速在[30,40]的汽車約有( )
太原市某時段100輛汽車通過祥云橋時,時速的頻率分布直方圖如圖所示,則時速在[30,40]的汽車約有( )| A. | 30輛 | B. | 35輛 | C. | 40輛 | D. | 50輛 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{15}{4}$ | B. | $\frac{13}{4}$ | C. | $\frac{12}{5}$ | D. | $\frac{13}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 直線 | B. | 圓 | C. | 雙曲線 | D. | 拋物線 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?x≤0,ex≤x+1 | B. | ?x≤0,ex>x+1 | C. | ?x>0,ex≤x+1 | D. | ?x>0,ex≤x+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com